여러가지 GD(Gradient Descent)에 대해 알아보자

여러가지 GD(Gradient Descent)에 대해 알아보자

알아볼 Gradient 종류는 아래와 같습니다. 위에서부터 아래로 파생되었다?고 생각하시면 될 것 같습니다..! 간단한 특징들을 공부하면서 정리했던 것들을 공유드리겠습니다.

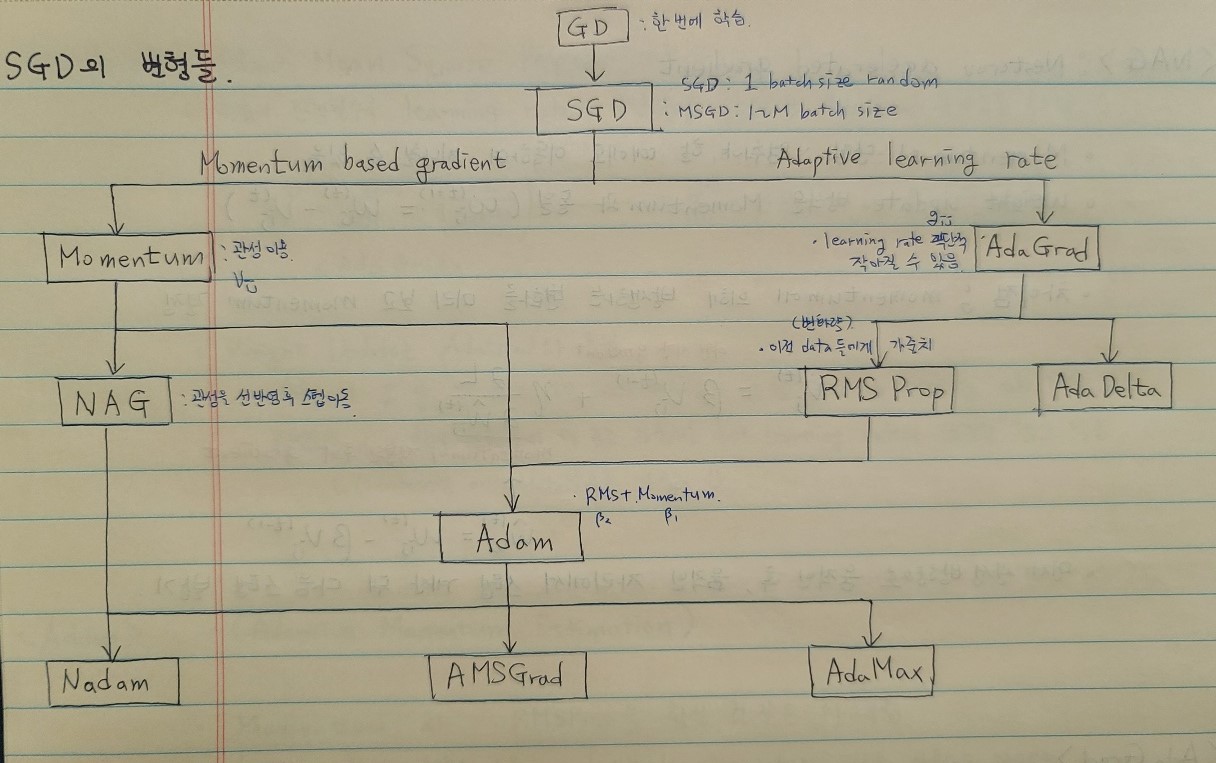
최대한 발전?의 순서대로 적어보겠습니다..

Batch Gradient Descent (BGD)

• Batch size = Training set size
• 수렴이 안정적이지만 메모리가 매우 많이 필요하며 긴 시간이 소요된다.

Stochastic Gradient Descent (SGD)

• Batch size가 1인 Gradient Descent
  • 전체 training set 중 하나의 data를 랜덤하게 선택
• 수렴에 Shoothing이 발생!
  • Shoothing이란, 기울기의 방향이 데이터마다 크게 변하는 걸 의미한다. Global minimum에 수렴하기는 어려울지라도, local minimum에 빠질 확률 줄어듦
• 1개씩 처리하므로, 벡터화 과정에서 속도를 잃으며 GPU 병렬 처리 활용 불가

Mini-Batch Stochastic Gradient Descent (MSGD)

• 전체 training set을 1~M 사이의 적절한 batch size로 나누어 학습한다.
  • batch size는 사용자가 지정
• Training set의 크기가 클 경우, BGD보다 속도 빠름

• Shoothing이 적당히 발생 (Local minimum 어느정도 피할 수 있음)

• i번째 뉴런의 j번째 weight의 업데이트 : $w^{(t+1)}{ij}$ = $w^{(t)}{ij} - \eta \frac{\partial L}{\partial w^{(t)}_{ij}}$
  • $\frac{\partial L}{\partial w^{(t)}_{ij}}$ 가 gradient며 weight를 어느 방향으로 업데이트할 지를 결정
  • L : loss function
  • $\eta$ : learning rate
• (M)SGD의 문제점
  • Mini-batch로 학습하는 경우 최적의 값을 찾아가기 위한 방향 설정이 뒤죽박죽임
  • Step size(=learning rate)에 매우 민감
    • very high learning rate : 급격하게 치솟음
    • high learning rate : 떨어지다가 어느 구간에 수렴
    • good learning rate : 잘 수렴
    • low learning rate : 매우 천천히 수렴
• 따라서, SGD의 변형들이 제안되었다. 크게 변형의 부분을 두 가지로 볼 수 있는데 아래와 같다. 이 두 가지의 변화를 중점으로 살펴보고자 한다.
  • Momentum 변화
  • Learning rate 조절

Momentum

• 이전 시간의 gradient까지 고려하여 weight 업데이트

• $w^{(t+1)}{ij} = w^{(t)}{ij} - v^{(t)}_{ij}$
  • $v^{(t)}_{ij}$ 항을 momentum이라고 한다. 이 momentum을 통해 이전 시간의 gradient를 반영한다. 식은 아래와 같다.
  • $v^{(t)}{ij} = \beta v^{(t-1)}{ij} + \eta \frac{\partial L}{\partial w^{(t)}_{ij}}$
  • 앞 항은 이전 시간의 gradient를 의미하며 여기서의 베타(=이전 gradient의 영향력)는 주로 0.9를 사용한다.
  • 뒷 항은 현재 시간의 gradient를 의미한다.
  • 따라서 여러번의 업데이트를 거친 경우의 수식은 아래와 같다.
    • $v^{(t)}{ij} = \eta \frac{\partial L}{\partial w^{(t)}{ij}} + \beta \eta \frac{\partial L}{\partial w^{(t-1)}{ij}} + \beta^{2} \eta \frac{\partial L}{\partial w^{(t-1)}{ij}} + \cdots$
    • 이전의 움직임을 유지(관성)
• 특징
  • Local minimu, 회피할 수 있음
  • Global Minimum을 무조건 찾는건 아님
  • Local minimum 피하자고 Momentum을 사용하지는 않음
  • 스텝 계산하여 움직인 후, 이전에 내려오던 관성방향으로 다음 스텝 밟음

Nesterov Accelerated Gradient (NAG)

• Momentum의 단점 : 멈춰야 할 때에도 이동하여 지나칠 수 있음
• weight update 방식은 Momentum과 동일 ($w^{(t+1)}{ij} = w^{(t)}{ij} - v^{(t)}_{ij}$)
• 차이점은 momentum에 의해 발생하는 변화를 미리 보고 momentum을 결정!
  • $v^{(t)}{ij} = \beta v^{(t-1)}{ij} + \eta \frac{\partial L}{\partial \hat{w}^{(t)}_{ij}}$
  • $w$ 에 hat이 달린 차이가 있다 momentum이 적용된 후의 gradient이며 식은 다음과 같다.
    • $\hat{w}^{(t)}{ij} = w^{(t)}{ij} - \beta v^{(t-1)}_{ij}$
• 먼저 관성 방향으로 움직인 후, 움직인 자리에서 스텝 계산 뒤 다음 스텝을 밟는 것

AdaGrad

• weight 업데이트 시, 각 weight마다 적합한 learning rate를 자동으로 설정
• 학습 과정에서, 변화가 많았던 매개변수들은 optimal 근처에 있을 확률이 높다! 따라서 learning rate를 작게하여 더욱 세밀히 업데이트!
• 학습 과정에서, 변화가 적었던 매개변수들은 optimal에서 멀리 벗어나 있을 확률이 높다! 따라서 learning rate를 크게하여 더욱 빨리 수렴하도록!
• 매개변수의 gradient $\frac{\partial L}{\partial w^{(t)}_{ij}}$ 는 “현재 시간에 얼마나 많이 변화되었는지를 나타내는 값”이이기 때문에
  • AdaGrad는 매개변수가 현재 시간까지 얼마나 많이 변화되었는지를 $g^{(t)}_{ij}$ 로 표현
  • $g^{(t)}{ij} = g^{(t-1)}{ij} + (\frac{\partial L}{\partial w^{(t)}{ij}})^{2} \to w^{(t+1)}{ij} = \frac{\eta }{\sqrt{g^{(t)}{ij}}+\varepsilon }\frac{\partial L}{\partial w^{(t)}{ij}}$
  • $g^{(t-1)}_{ij}$ : 이전 시간까지 얼마나 변회되었는지
  • $\frac{\partial L}{\partial w^{(t)}_{ij}}$ : 현재 시간에 얼마나 변화되었는지
  • $\varepsilon$ : $1-^{-8}$ , 0으로 나누는 것 방지
  • 현재 시간까지 얼마나 변했는지의 $g^{(t)}_{ij}가 클수록 전체 learning rate가 작아지는 것 알 수 있음
• 특징
  • learning rate를 직접 조절하지 않아도 되는 장점
  • 학습이 오래 진행될 경우, 변수의 update가 이루어지지 않는다는 단점
  • $g_{ij}$ 는 $()^{2}$가 들어가기 때문에 계속 증가하기 때문에 learning rate가 계속 감소한다. 즉 바로 윗줄과 같이 update가 이루어지지 않음
  • 추후 AdaDelta와 RMS Prop으로 단점을 극복

Root Mean Square Propagation (RMSProp)

• 학습이 진행될수록 learning rate가 극단적으로 감소하는 AdaGrade의 문제점을 해결
  • $g^{(t)}{ij} = g^{(t-1)}{ij} + (\frac{\partial L}{\partial w^{(t)}{ij}})^{2} \to g^{(t)}{ij} = \beta g^{(t-1)}{ij} + (1 - \beta ) (\frac{\partial L}{\partial w^{(t)}{ij}})^{2}$
  • $\beta$ : 가중치 부여, 시간이 지날수록 오래된 data의 영향이 줄어들도록 설계 = 가중 평균 방식
• Weight Update는 AdaGrad와 동일
  • AdaGrad : $g_{ij}$ 는 현재 시간까지의 변화량의 합으로 정의 -> learning rate 계속 감소
  • RMSProp : 현재 변화량에 더 높은 가중치를 주어 learning rate의 급격한 감소를 막음
    • Momentum처럼 예전 data일수록 가중치 감소

Adaptive Momentum Estimation (Adam)

• Momentum과 RMSProp을 합친 것 같은 알고리즘
  • Momentum : 이전 gradient의 경향을 사용
  • RMSProp : 이전 learning rate의 경향을 사용하는 알고리즘
• (gradient의 경향) : $v^{(t)}{ij} = \beta{1} v^{(t-1)}{ij} + (1 - \beta{1})\frac{\partial L}{\partial w^{(t)}_{ij}}$
• (learning rate의 경향) : $g^{(t)}{ij} = \beat{2} g^{(t-1){ij} + (1 - \beta{2})()\frac{\partial L}{\partial w^{(t)}_{ij}})^{2}$
  • 일반적으로 $\beta_{1}$ 은 0.9, $\beta_{2}$ 는 0.99를 사용
• Adam 논문에서는 $v_{ij}$ , $g_{ij}$ 를 unbiased expectation 형태로 이용하기 위해 아래처럼 변형
  • $\hat{v}^{(t)}{ij} = \frac{v^{(t)}{ij}}{1-\beta^{t}{1}}$ , $\hat{g}^{(t)}{ij} = \frac{g^{(t)}{ij}}{1-\beta^{t}{2}}$
  • $\beta^{t}{1}$ 와 $\beta^{t}{2}$ 는 각 $\beta_{1}$ 과 $\beta_{2}$를 t번 곱한 것
• 최종 weight update 식은 아래와 같다.
  • $w^{(t+1)}{ij} = w^{(t)}{ij} - \frac{\eta }{\sqrt{\hat{g}^{(t)}{ij}}+\varepsilon} \hat{v}^{(t)}{ij}$