Linear Regression (2)작성중 - Machine Learning
Updated:
이번 포스팅은 Linear Regression에 대해 포스팅하는 두 번째 시간입니다.
본 포스팅은 광운대학교 정한울 교수님 머신러닝 과목을 바탕으로 작성을 하였습니다.
지난 포스팅에 이어서 Gradient Descent Method에 대해 설명하겠습니다.
Gradient Descent Method
- $MSE(\textbf{w}) = \frac{1}{N}\sum_{i = 1}^{N}(y_{i}-\mathbf{w}^{T}x_{i} )^{2}$
- $w_{next} = w_{present} - \eta \bigtriangledown MSE(\mathbf{w})$, $\eta$ = learning rate
MSE가 convex하다면, 훨씬 시간이 단축되며 learning rate란 $\bigtriangledown MSE$가 0이 되는 속도를 의미한다고 생각하시면 됩니다. 그러므로 굉장히 중요한 파라미터가 됩니다.
Learning rate
- 일반적으로 큰 learning rate부터 시작하여 점점 작은 값으로 변경하며 learning schedule이라고 부름

Gradient Descent Method vs. Stochastic Gradient Descent
Data가 매우 많다고 가정을 하게 되면 Gradient Descent도 모든 data에 하게 됩니다. 하지만 모든 Data에 적용을 하면 매우 오래 걸리며 연산량도 많아집니다. 그래서 Stochastic Gradient Descent라는 개념이 나왔는데요. 매 step마다 random하게 골라 업데이트를 진행하게 됩니다. 대신에 불안정하며 learning rate가 매우 중요하게 됩니다. learning schedule을 매우 잘 잡아야 되겠죠? 추가적으로 Mini batch Gradient Descent라는 개념도 있습니다.
Linear Regression with Gaussian Distribution Likelihood
실제로 정답을 내릴 때 그렇다 아니다로 매기는 것보다 이것일 확률이 몇 %다라고 말하는 것이 더 정확할 것입니다. 실제로 모든 것은 확률에 의해 결정된다고 해도 과언이 아닙니다. 그렇기 때문에 마찬가지로 머신러닝에서도 확률이 아주 기본중에 기본입니다.
- linear regression이 가우시안 분포의 형태를 가지는 모델일 때
x : data , $\theta$ : model , N : Gaussain
이 모델의 파라미터를 추정하는 다음과 같이 MLE를 사용하는 것이었습니다.
$\hat{\theta} \equiv arg\underset{\theta}{max}logp(D|\theta)$
우변의 log 텀이 최대가 되는 $\theta$를 찾는 것이었습니다.
그리고 일반적으로 학습하는 예제가 독립적이고 동일하게 분포되어 있다고 가정하기 때문에 다음과 같이 정의할 수 있습니다.
log-likelihood의 의미를 가지는
$\mathit{l}(\theta) \equiv logp(D|\theta) = \sum_{i=1}^{N}logp(y_{i}|\boldsymbol{x_{i}},\theta)$
식으로 표현할 수 있습니다. sum이 최대가 되는 것에 집중하여 보시면 됩니다.
MLE 유도하기
위 식에 가우시안 정의를 대입하여 보면 다음과 같이 유도할 수 있습니다.
기존의 가우시안 식에서 평균 $\mu = \mathbf{w}^{T}\textbf{x}_{i}$이라고 보시면 됩니다. 정리된 식에서 보면 RSS를 최대로 하면 되며 즉, Normal equation으로 풀면 된다는 것을 알 수 있습니다. Normal equation이 잘 기억이 안 나신다면 이전 포스팅을 참고하시기 바랍니다.
Normal equation 식은 다음과 같습니다.
Regression model의 noise
그러면 linear regression에서의 noise는 어떠한 분포를 띌 지 확인해보도록 하겠습니다.
만약 에러를
라고 정의를 하면 RSS식은 다음처럼 표현할 수 있습니다.
그렇다면 regression model의 noise은 일정한 분산을 가진 zero-mean gaussian 분포를 따른다고 할 수 있습니다.
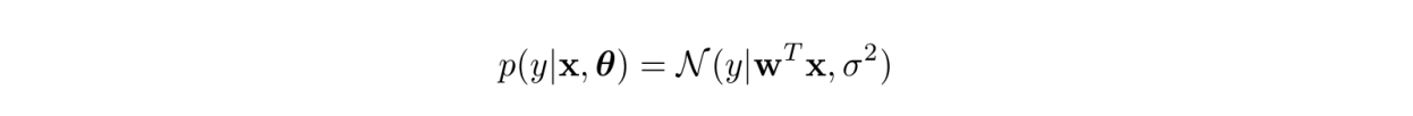
Leave a comment