Linear Regression (1) - Machine Learning
Updated:
이번 포스팅은 Linear Regression에 대해 포스팅하겠습니다.
본 포스팅은 광운대학교 정한울 교수님 머신러닝 과목을 바탕으로 작성을 하였습니다.
Linear Regression에 들어가기 앞서 먼저 알아야할 것들에 대해 미리 알아보는 시간을 가지도록 하겠습니다. 일단 base로 알아야할 것이 선형대수학인데요. 그 이유가 바로 Matrix와 Vector의 사용때문입니다.
Vextor & Matrix
이전 포스팅들에서 언급한 것처럼 붓꽃을 분류하는 알고리즘에 대해 말하자면, 분류할 수 있는 특징이 꽃잎의 너비와 길이, 꽃받침의 너비와 길이. 이렇게 4개의 특징을 가지고 분류를 하게 되는데 vector로 표현을 하게 됩니다. 이러한 data가 1개가 아니라 무수히 많으니 매번 수많은 값을 표기하는 것이 아니라 Matrix로 간단하게 표현하다고 생각하시면 쉽게 이해할 수 있습니다.
보통 하나의 feature vector는 column vector로 표현하는데요, 데이터 개수를 N개라고 하면 $\mathbf{X}$ = $\mathbf{x}_{1}^{T}$ … 로 정의가 가능하며 design matrix라고 부릅니다. size는 N x D가 되겠습니다. 또한 이 Design matrix를 weight matirx와 곱하게 되고 이 weight 값을 변경하여 각각의 중요도를 바꾸는 것이고 model을 수정한다고 말씀드렸습니다.
Linear Regression 예
- 공부시간 vs. 시험 점수
- (지역, 상권, 교통) vs. 집값
- (키, 몸무게, 운동시간) vs. 신체 나이
이렇게 결과로 연속적인 값이 나온다고 보시면 됩니다. 공부시간처럼 input이 1차원으로 이루어진 것을 linear Regression이라고 합니다. 집값이나 신체나이의 경우처럼 input의 차원이 높아지는 경우도 있는데요. 2차원인 경우는 multi-dimension, 3차원 이상부터는 hyper-demension이라고 부르며, 추가적으로 $\hat{y} = a_{1}x_{1} + a_{2}x_{2} + a_{3}mx_{1}^{2}$처럼 제곱 이상이 들어간 경우를 polynomial regression이라고 부릅니다.
Linear Regression model
.
- $\hat{y}$ = 모델이 예측한 값
- $D$ = feature의 수
- $x_{i} = i^{th}$ feature value
- $\theta_{j} = j^{th}$ model parameter
- $\theta_{0}$ = bias
$\hat{y}$는 model이 예측한 값이지 정답을 말하는 것이 아님을 주의해야 합니다. 또한, bias값 때문에 matrix의 곲을 진행할 때에는 실제로 없는 $x_{0}$을 만들고 1값으로 해줘야합니다. 아래 식은 벡터로 표현한 식입니다. 참고하시면 됩니다.
$\hat{y} = h_{\theta}(\mathbf{x}) = \mathbf{\theta}^{T}\mathbf{x} = \begin{bmatrix}
\theta_{0} & \theta_{1} & \theta_{2} & \theta_{3}
\end{bmatrix}
\begin{bmatrix}
x_{0}=1
x_{1}
x_{2}
x_{3}
\end{bmatrix}$
- $h_{\theta}$ : hypothesis function with model parameter vector $\theta$
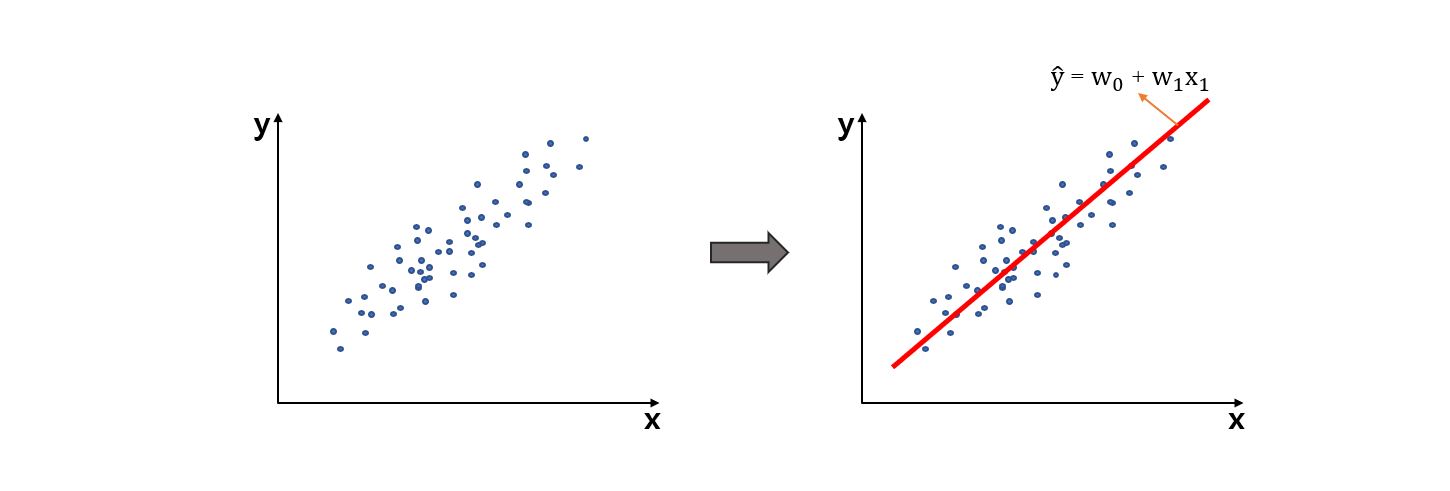
이제 개념은 얼추 잡았으니 어떻게 모델이 학습되는지 알아야겠죠? 학습은 주어진 데이터에 가장 적합한 MLE의 선형 곡선을 결정해야합니다. 즉 $\hat{y}$을 올바르게 정해야합니다. N=1(feature vector가 1일 때)를 예로 들어 보겠습니다. 이때의 예측값 $\hat{y}$은
이며 우리는 아래 그림처럼 data의 분포를 최대한 만족하는 $\mathbf{w}$을 결정해야 합니다.
참고로 $\vec{\theta} = (\theta_{0}, \theta_{1})$를 linear regression에 한해서는 w라고 합니다!
Residual Sum of Squares
위에서 $\hat{y}$은 예측값이라고 말씀드렸습니다. 그러면 이 예측값이 정답에 가까워져야할텐데 실제 정답과 얼마나 다른지를 비교해야 합니다. 이 값을 error라고 하며 $Error = y - \hat{y}$ 로 정의합니다.
그리고 모든 Data에 해야하므로 총 에러는
로 정의할 수 있습니다! 그리고 이것을 RSS(Residual sum of squares)라고 부릅니다. 제곱이 있는 것을 주의하면 될 것 같습니다. 다시 한 번 정리하면
RSS(w) = $\sum_{i=1}^{N}(y_{i} - \mathbf{w}^{T}\mathbf{x}_{i})^{2}$입니다.
또한, RSS에 평균을 낸 식이 어디선가 들어봤었던 MSE(Mean Square Error)라고 합니다.
우리는 이 RSS와 MSE를 loss function 혹은 cost function이라고 부릅니다. 그리고 이것을 data에 대해 model을 fit할 때 평가합니다. 에러가 작을수록 잘 fit한 것이겠죠? 참고로 RSS와 MSE는 수 많은 loss function 중에 하나라고 보시면 되고 실제로는 무수히 많습니다.
Finding the MLE
이전에 배운 Best fit curve인 MLE를 찾기 위해서는 MSE를 최소화해야합니다. $\mathbf{w}$값에 따라 MSE가 바뀌고 우리는 이 에러를 최소화하는 것이 목표이기 때문입니다. 그리고 최소화하기 위해서는 gradient를 구해서 최소가 되는 지점을 찾아야겠습니다. 정리해보겠습니다.
- MLE를 찾기 위해서는 MSE를 최소화
- MSE를 최소화하기 위해서는 MSE의 gradient를 구해야 함
그러면 이제 gradient를 구해보겠습니다.
gradient of MSE = $(\frac{\partial MSE}{\partial w_{0}}, \frac{\partial MSE}{\partial w_{1}} ,… ,\frac{\partial MSE}{\partial w_{N}}) = -\frac{2}{N}\sum_{i=1}^{N}(y_{i} - \mathbf{w}^{T}\mathbf{x}{i})\mathbf{x}{i}$이며 $= \vec{0}$을 만족하는 지점이 최소화인 지점일 것입니다.
$\frac{2}{N}$은 필요 없으니 잠시 무시하고 분배 법칙을 사용하여,
정리하면,
이 됩니다. 이 식을 만족하는 w를 찾으면 문제가 해결되겠죠?? N-dimensional vector $\mathbf{y} = [y_{1},y_{2},…,y_{N}]^{T}$ 와 미리 정의한 design matrix X의 정의로 다음과 같이 최종 식을 정리할 수 있습니다.
$\mathbf{X}^{T}\mathbf{X}\mathbf{w} = \mathbf{X}^{T}y$ 로 하며 Normal eqauation 이라고 정의합니다. 이 식을 만족하는 w를 찾아야합니다. 이 w 식을 찾게 해주는 식을 Normal equation이라고 하는 겁니다.
그리고 이 Normal equation를 만족하는 w를 $\hat{\mathbf{w}}{OLS}$라고 하며 $\hat{\mathbf{w}}{OLS} = (\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}y$로 구할 수 있습니다. 우변에 있는 값들은 모두 일고 있는 것들이므로 직선을 바로 구할 수 있겠습니다. 하지만 차원 D, data 개수 N이 매우 클 때 이렇게 w를 구하는 것은 매우 복잡합니다. 그리고 아래와 같은 문제점이 또 발생할 수 있습니다.
- MSE가 convex하지 않을 수 있다.
- 고차원이면 OLS solution이 나오지 않을 수 있다.
- Data가 많으면 매우 어렵다.
그러면 공식 말고 찾을 수 있는 방법이 없을까요?? 있습니다!
MSE의 gradient 를 구하는 식에서 미분 값이 0벡터이어야 한다고 말씀을 드렸었습니다. 즉, 0이 되는 지점을 찾는것이죠. 그러면 만약 현재 값에 대해 gradient를 구했을 때, + 혹은 - 값을 가진다면 그 반대값을 더해준다면 0을 찾을 수 있지 않을까요? 음수면 증가시키고 양수면 감소시킨다면 0을 찾을 수 있을 겁니다. 이것이 흔히 알고있는 Gradient Descent Method입니다.
Gradient descent method부터는 다음 포스팅에 이어서 하도록 하겠습니다. 감사합니다.
Leave a comment