평면에 내린 수선의 발 구하기 + 평면에 대칭인 점 구하기

평면에 내린 수선의 발 구하기 + 평면에 대칭인 점 구하기

점 $A(\vec{a})$ 에서 점 $P(\vec{p})$ 를 지나고 법선 벡터가 $\vec{h}$ 인 평면 $\pi$ 에 내린 수선의 발 $H(\vec{h})$ 구하기

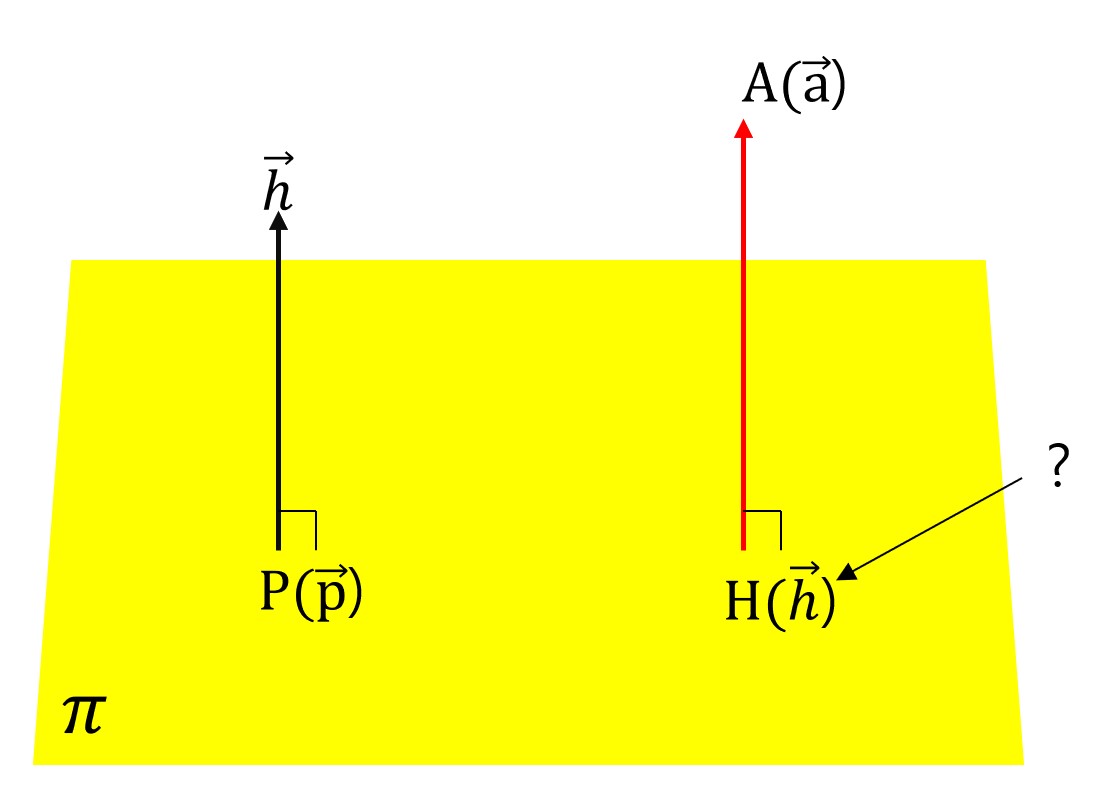
점 H가 $\pi$ 에 있으므로 식 1은 ( $\vec{h}$ - $\vec{p}$ ) $\cdot$ $\vec{h}$ = $0$

$\pi$ 의 법선과 $\overline{AH}$ 가 평행하므로 $\vec{h}$ - $\vec{p}$ = $k\vec{h}$ 이다. 따라서 식 2는 $\vec{h}$ = $\vec{a}$ + $k\vec{h}$

식 2를 식 1에 대입을 하면, ( $\vec{a}$ + $k\vec{h}$ - $\vec{p}$ ) $\cdot$ $\vec{h}$ = $0$ 이고 전개하면 아래의 식을 구할 수 있다.

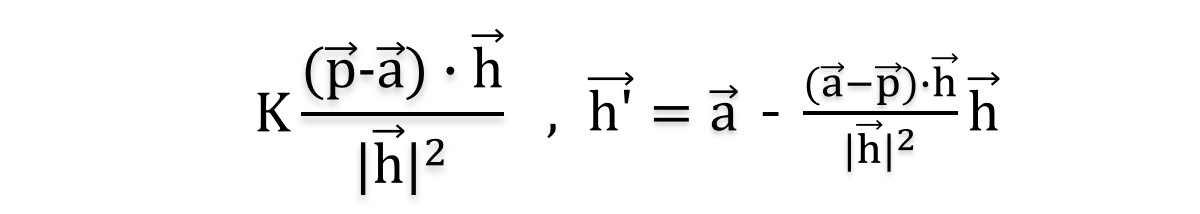
여기서 분자의 식을 평면의 방정식으로 변환할 수 있다.

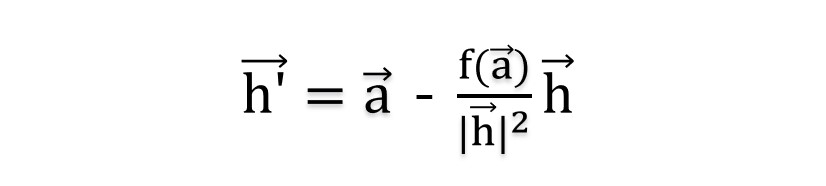
여기서 $\vec{a}$ 는 대칭할 점, $\vec{h}$ 는 normal vector, f() 는 평면의 방정식이다.

이때 평면의 방정식을 대입하여 구한 수선의 발 $\vec{h’}$ 가 (x’, y’, z’) 라고 할 때, 점 a = (a, b, c)에 대한 대칭점을 (a’, b’, c’) 라고 하자. 그렇다면 수선의 발 (x’, y’, z’) 은 다음의 식을 만족하게 된다.
(x’ = $\frac{a+a’}{2}$ , y’ = $\frac{b+b’}{2}$ , z’ = $\frac{c+c’}{2}$ )

다르게 말해서, 한 점과 그 점의 수선의 발을 안다면 해당 평면에 대칭된 점의 위치는 아래와 같다.

(a’, b’, c’) = (2x’ - a, 2y’ - b, 2z’ - c)