Calibration이란? - OpenCV(C++)

Calibration 이론 공부하기

Calibration을 코드로 구현해보기 위해 공부한 것들을 정리해보았지만 여간 어려운게 아니었습니다..

틀린 부분이 있다면 댓글로 언제든지 환영입니다! 그럼 이제 시작해보겠습니다.

공부한 곳

https://darkpgmr.tistory.com/32 https://computervision.tistory.com/2 https://m.blog.naver.com/PostView.nhn?blogId=jinhuk1313&logNo=220592125874&proxyReferer=https:%2F%2Fwww.google.com%2F

1. Calibration 정의

카메라로 촬영을 하게 되면 실세계인 3D에서 이미지인 2D로 담겨지게 되어 차원이 낮아진다고 볼 수 있습니다. 즉, 카메라 영상에서는 3D상의 점을 2D의 이미지 평면에 투사함으로 얻어집니다. 그러면 실세계의 3D 점은 이미지의 2D에서 어떻게 정의될까라는 물음에서 시작합니다. 정답은 촬영 당시의 카메라의 위치, 방향에 의해 결정된다는 것입니다. 하지만 이 점들은 카메라의 내부적인 조건에 의해 크게 영향을 받을 수 있습니다.

1.1 내부 요인

• 렌즈의 종류
• 렌즈와 이미지 센서 사이의 거리
• 렌즈와 이미지 센서 사이의 각도

이러한 내부적인 요인들의 파라미터를 구하는 과정을 Calibration이라고 합니다. 궁극적으로는, 이러한 파라미터를 통해 카메라 왜곡을 잡는 작업을 Calibration이라고 하는 것 같습니다.

1. Calibration 식에 대해

식을 통해 자세히 알아보도록 하겠습니다. 식은 다음과 같습니다.

• x, y : 카메라 좌표계의 좌표
• A : Intrinsic Camera Matrix (내부 파라미터)
• [R|t] : 회전/이동 변환 행렬 (외부 파라미터)
• X, Y, Z : 월드 좌표계 상의 3D 점의 좌표

여기서 카메라 좌표계가 이미지 2D의 좌표이고 (X, Y, Z)를 실세계의 좌표라고 보시면 됩니다. 그리고 A와 [R|t] 를 합쳐 Camera Matrix 또는 Projection Matrix라고 부릅니다.

1. 카메라 내부 파라미터 (Intrinsic Parameters)

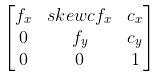
3.1 초점 거리 (Focal length)

$f_{x}$ 와 $f_{y}$ 입니다. 카메라 모델에서는 상대적인 개념으로 렌즈 중심과 이미지 센서와의 거리를 나타냅니다. 동일한 카메라라도 해상도가 바뀐다면 초점거리도 바뀝니다. 그리고 헷갈리지 말아야 할 것이 초점 거리 f는 픽셀(pixel) 단위로 표현한다는 것입니다. 이것은 초점 거리 f가 이미지 센서의 셀(cell) 크기에 대한 상대적인 값으로 표현된다는 의미입니다. 이미지의 픽셀은 이미지 센서의 cell에 대응한다는 말 또한 동일한 말입니다.

• $f_{x}$ : 초점 거리가 가로 방향 셀(cell) 크기의 몇 배인지를 나타내는 값
• $f_{y}$ : 초점 거리가 세로 방향 셀(cell) 크기의 몇 배인지를 나타내는 값
• 일반적으로, f = $f_{x}$ = $f_{y}$

예를 들어, cell의 크기가 0.1mm, f = 500pixel인 경우에 카메라의 렌즈 중심에서 이미지 센서까지의 거리는 0.1*500 = 50mm가 됨을 확인할 수 있습니다. 픽셀 단위로 표현하는 이유는 영상에서 기하하적 표현을 용이하게 하기 위함이라고 합니다.

Nomalized Image Plane

• 초점으로부터 거리가 1(unit distance)인 평면
• 이 평면 상의 좌표를 Normalized Image Coordinate라고 함
• 가상의 이미지 평면

3.2 주점 (Principal point)

$c_{x}$ 와 $c_{y}$ 이며 카메라 렌즈의 중심입니다. 다르게 말하면, 핀홀에서 이미지 센서에 내린 수선의 발의 영상 좌표라고 할 수 있습니다. 영상 중심점과는 엄연히 다르며 단위는 픽셀입니다. 영상의 모든 기하학적 해석은 이 주점을 이용하여 이루어진다고 합니다.

3.3 비대칭 계수 (skew coefficient)

skew_c로 부르며 이미지 센서의 cell array에서 y축이 기울어진 정도이나 최근 카메라는 이러한 에러가 거의 없다고 하여 고려하지 않는다고 합니다.

카메라 좌표계 ($(X_{c}, Y_{c}, Z_{c})$)에서 normalized image plane 상의 좌표로 변환하여 (u = $\frac{X_c}{Z_c}$ , v = $\frac{Y_c}{Z_c}$ )이 되고 우리가 원하는 이미지 평면에서의 영상좌표(pixel)을 구하기 위해 focal length f를 곱하여 (x = $\frac{X_c}{Z_c}f_x$ , y = $\frac{Y_c}{Z_c}f_y$ )를 구합니다. 여기서 x, y는 이미지 중심에서부터의 거리가 아니라 좌상단이 기준입니다. 최종적인 영상 좌표는 x, y에 각각 주점인 $c_{x}$ 와 $c_{y}$ 를 더하면 됩니다. 즉, 최종 영상 좌표는 (x = $\frac{X_c}{Z_c}f_x + c_{x}$ , y = $\frac{Y_c}{Z_c}f_y + c_{y}$ )입니다.

1. 카메라 외부 파라미터 (Extrinsic Parameters)

카메라 좌표계와 월드 좌표계 사이의 변환 관계를 설명하는 파라미터이며 두 좌표계 사이의 회전(rotation) 및 평행 이동(translation) 변환으로 표현합니다. 구하는 방법은 다음이 필요합니다.

• Calibration을 이용하여 구해진 카메라 내부 파라미터
• Sample 혹은 미리 알고 있는 3D 월드좌표 - 2D 영상좌표 매칭 쌍들

이 2가지를 이용하여 변환 행렬 [R|t] 를 구합니다.

1. 왜곡
   카메라에 대해 숨은 내부 파라미터라고 볼 수 있는 왜곡입니다. 행렬 A(Intrinsic camera parameter)에는 들어가있지는 않지만 엄연히 존재합니다.

• 방사 왜곡 (radial distortion)
• 접선 왜곡 (tangential distortion)

5.1 방사 왜곡 (Radial distortion)

• 직선을 곡선처럼 보이게 하는 왜곡
• $x_{corrected} = x(1 + k_{1}r^{2} + k_{2}r^{4} + k_{3}r^{6})$
• $y_{corrected} = y(1 + k_{1}r^{2} + k_{2}r^{4} + k_{3}r^{6})$

5.2 접선 왜곡 (Tangential distortion)

• 렌즈가 잡아낸 이미지와 이미지 평면이 평행하지 않아 발생하는 왜곡
• $x_{corrected} = x + [2p_{1}xy + p_{2}(r^{2} + 2x^{2})]$
• $y_{corrected} = y + [p_{1}(r^{2} + 2y^{2}) + 2p_{2}xy]$

이렇게 2개의 왜곡이 있습니다. 그래서 왜곡 파라미터는 다음과 같으며, 방사 왜곡에 포함된 r은 다음의 파라미터를 통해 구할 수 있습니다.

• Distortion coefficient = (k_{1} k_{2} p_{1} p{2} k_{3})