DLT - Camera Calibration (Photogrammetry)
Updated:
DLT - Camera Calibration 공부하기
본 포스팅은 Cyrill Stachniss 교수님의 강의를 바탕으로 작성하였습니다.
강의 출처 : https://www.youtube.com/watch?v=3NcQbZu6xt8
수식 issue가 있어서 Cyrill Stachniss 교수님의 강의자료를 수정 후 올립니다.
Direct Linear Transform
이전 Photogrammetry 포스팅의 내용을 기본으로 하니 앞선 포스팅을 참고하여 주시길 바랍니다.
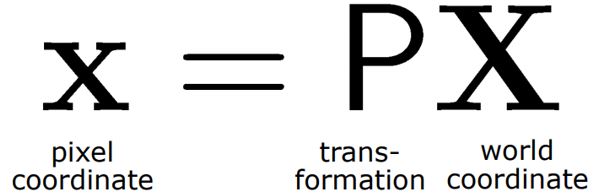
이전에 배웠던 것처럼 world 좌표에서 pixel 좌표로의 이동을 projection matrix P 로 설명을 했었습니다. 이걸 이용해서 오늘 DLT를 배워보려고 합니다.
목표를 설정해보겠습니다. 먼저 목표는 아래와 같습니다.
- WANTED : 카메라의 Extrinsics & Intrinsic Parameters
- GIVEN : Object points(= control points)의 좌표
- OBSERVED : 이미지의 알고있는 3D 좌표의 좌표(x, y)
여기서 control point란 이미지에 어떤 점이 가지고 있는 world 의 좌표입니다. (x,y,z)가 되겠고 그거에 대한 이미지의 2D 좌표 또한 알고 있다고 가정합니다.
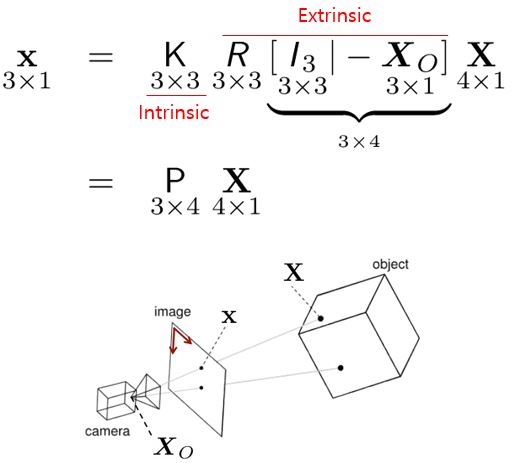
그러면 이전에 배웠던 DLT를 사용한 Mapping을 생각해보면 다음과 같습니다.
K는 Calibration Matrix이고 R은 Rotation Matrix, Xo는 Projection center입니다. 이 구성은 이전 포스팅에서 다루었으니 생략하도록 하겠습니다. 총 파라미터 수는 몇개일까요?
11개의 파라미터를 estimate하는 것이 목표!
각 matrix에 대한 파라미터를 표시하였습니다. 이 파라미터를 구해야하는데 저희가 알고있는 것은 control point라고 생각하시면 됩니다. 그렇다면 결과적으로 몇 개의 point를 알아야 이 카메라의 파라미터를 구할 수 있을까요? 정답은 6개의 point입니다! 먼저 x=PX의 표현을 변형시켜가며 이미지 좌표의 $x$ 와 $y$ 를 표현해보겠습니다.
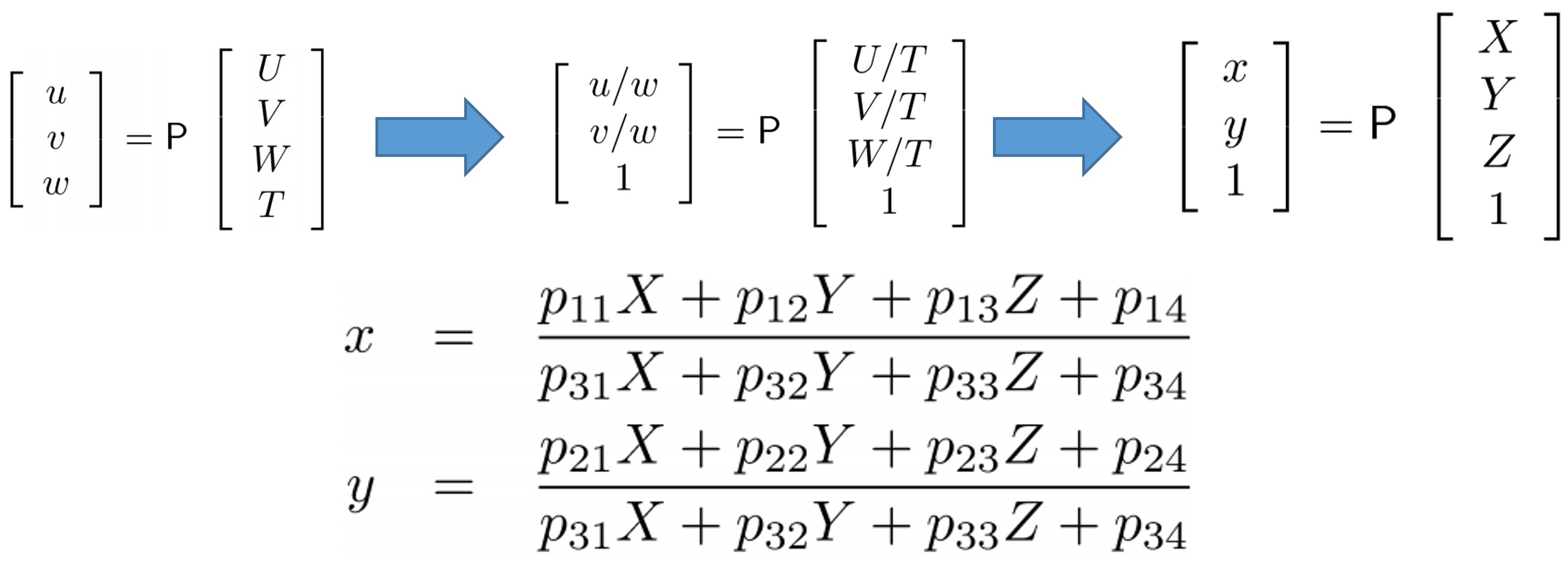
한개의 이미지에 대해 이미지 좌표 $x$ , $y% 는 위와 같이 P의 elements와 world 좌표 X,Y,Z 로 표현할 수 있습니다. 그렇다면 여러 개의 포인트를 알고 있다면 아래와 같이 식이 표현되겠죠! $i$ 는 알고있는 좌표의 수라고 생각하시면 됩니다.
그러면 DLT 식인 x=PX 를 rearrange 해보겠습니다. 새롭게 A,B,C matrix를 아래와 같이 정의하여 DLT 식을 A,B,C에 대해 다시 써보면 아래와 같습니다. 이미지 좌표 하나에 대한 식이라고 보시면 되겠습니다.
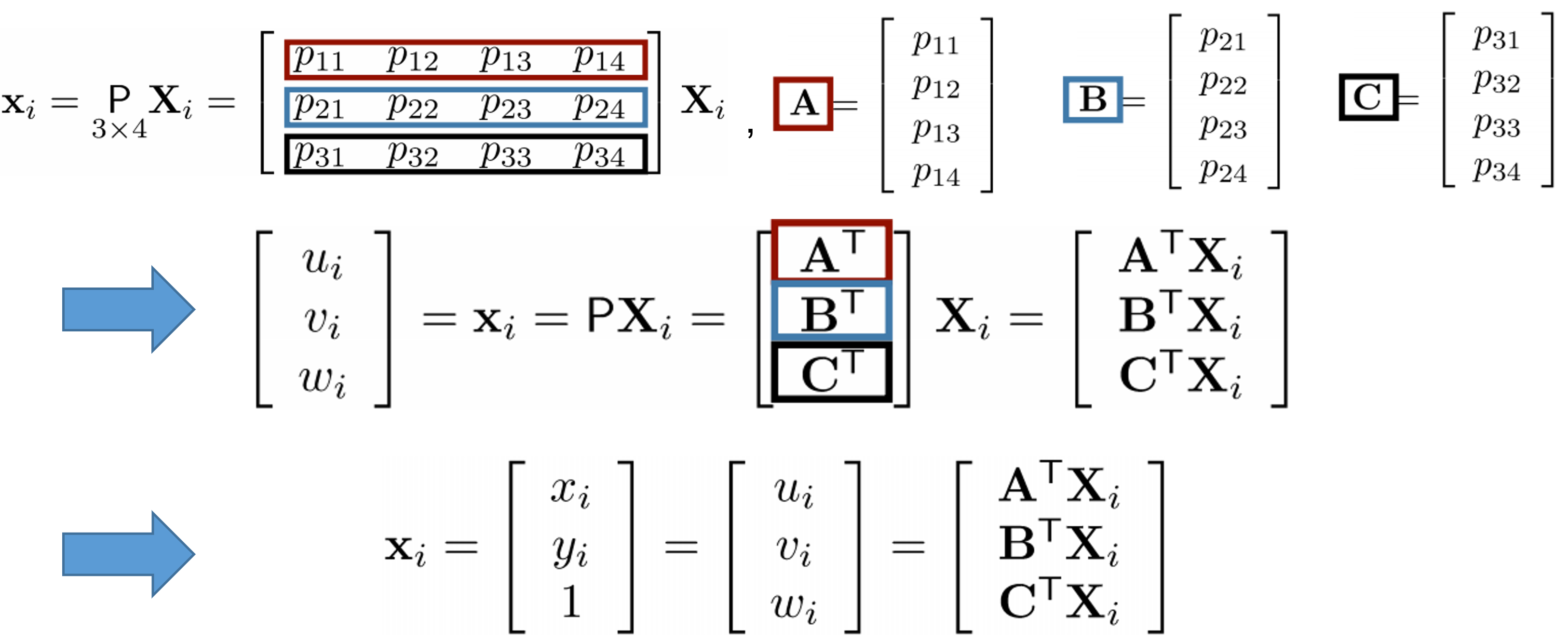
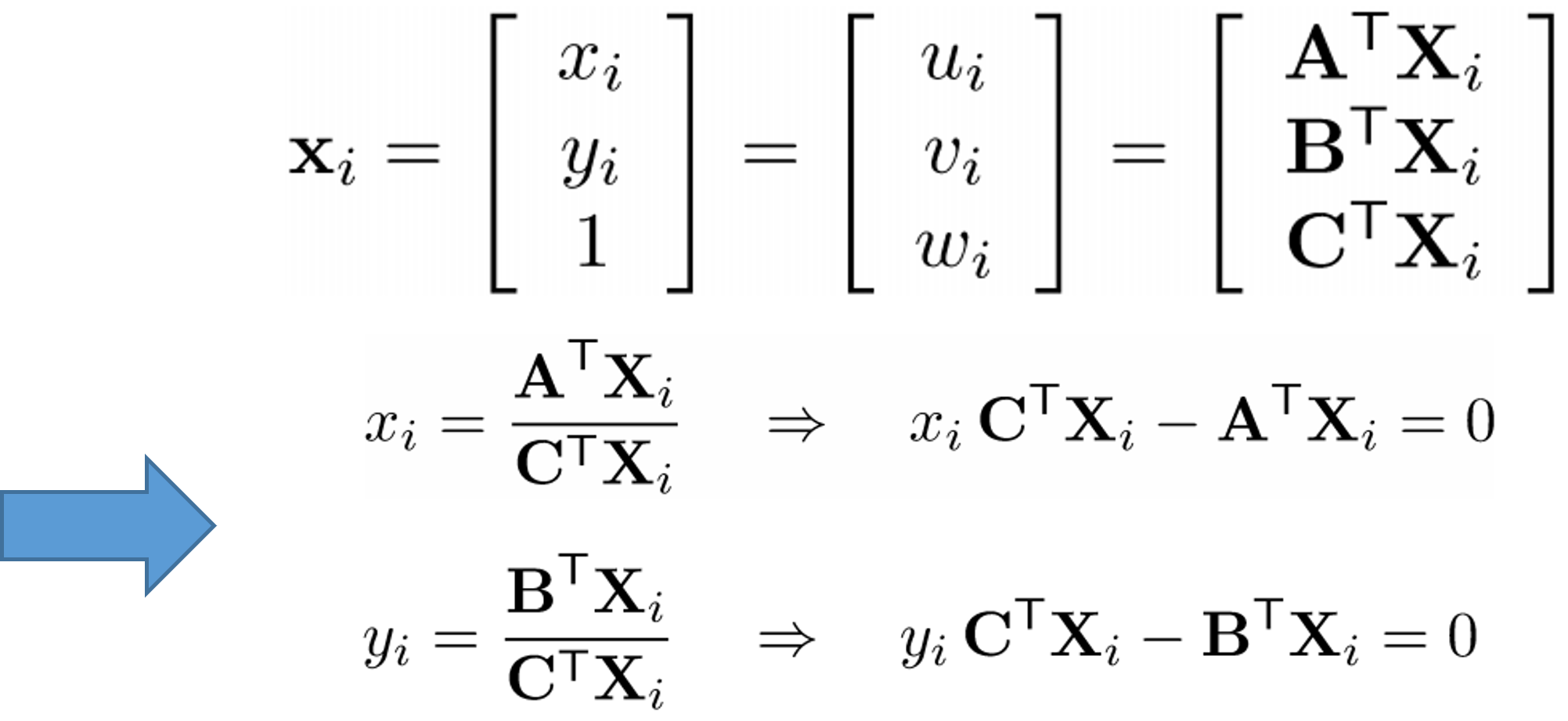
그렇다면 파라미터 A, B, C에 대해 linear equation 을 얻었습니다. 식을 보기 쉽게 아래로 표현해보겠습니다. 여기서의 $x_{i}$ , $y_{i}$ 는 알고 있는 값이라는 것을 주의하시길 바랍니다.
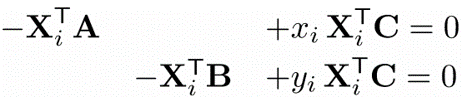
따라서, 실제로 Parameter vector $p$ 를 얻을 수 있다는 것을 의미합니다. $p$ 는 Projection Matrix P를 vector화 한 것이라고 생각하시면 됩니다. 수식은 아래와 같습니다.
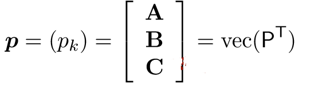
linear equation 을 vector $p$ 로 표현을 하면 아래와 같고 풀면 $p$ 가 A와 B, C를 포함하는 vector이므로 동일한 것을 알 수 있습니다.
여태까지 한 것을 정리해보겠습니다. 각 point에 대해 $a_{x_{i}}^{T}p = 0$ 과 $a_{y_{i}}^{T}p = 0$ 를 정의할 수 있고 $I$ 개의 point 를 한 번에 쓰면 아래와 같이 표현할 수 있겠습니다!
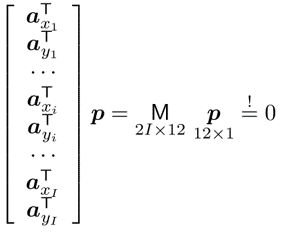
이제 이 식을 풀기만 하면 끝이겠죠?? 이 식은 Linear system Ax=0 을 푸는 꼴이며 동등하게 A의 null space를 찾는 것과 동일합니다. 따라서 $Mp = 0$ 을 SVD 에 적용할 수 있습니다. (SVD가 무엇인지는 여기서 다루지 않겠습니다.) 하지만 실제는 현실이기에 0이 아닌 어떠한 $\omega$ 값을 가지게 됩니다. 그렇기 때문에 $\Omega$ = $\omega^{T}$ $\omega$ 로 정의를 한 후 이때의 $p$ 를 최소화하게 되는 $\hat{p}$ 을 구하고 그것의 SVD를 구해 가장 작은 singular vector를 선택하고 그것을 $p$ 의 solution 으로 사용하게 됩니다. 수식으로 보겠습니다!
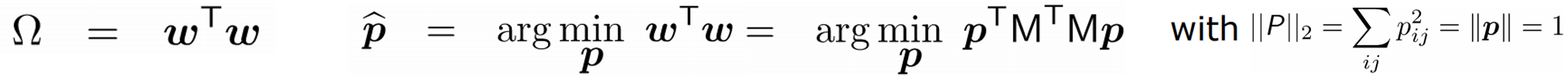
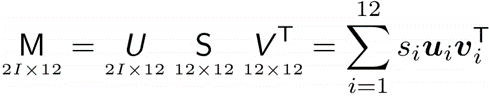
여기서 중요한 가정이 있습니다. M의 경우 gross error가 없다고 가정하며 6개 이상의 점을 안다고 했을 때 이 점들이 같은 평면에 없어야 한다는 점입니다. 같은 평면에 존재하게 되면 M의 행렬의 rank가 줄어들기(=rank deficiency) 때문이겠죠?
그러면 이제 P에서 K,R,Xo 를 구해야 합니다. 아래와 같이 새롭게 H를 정의하게 되면 Xo는 H로 표현이 가능합니다.
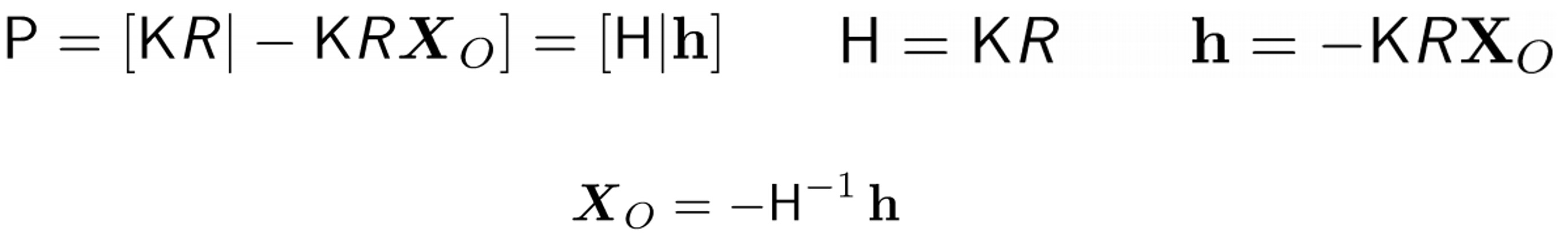
H=KR 을 자세히 살펴보면, K 는 3x3 triangular matrix이고 R 은 3x3 rotation matrix입니다. 여기서 Matrix를 triangular와 rotation matrix로 분해하는 decomposition이 있는데 무엇일까요?? 정답은 QR decomposition입니다.
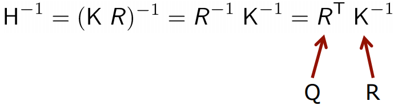
하나하나 구해봅시다.
- H=KR은 homogeneous matrix이므로 homogeneous normalize 필요
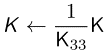
- Decompose하여 $H^{-1}$ = $R^{T}$ $K^{-1}$ 를 얻으면 K는 positive diagonal matrix
- 여기서 $K_{11}$ 와 $K_{22}$ 는 camera constant로 음수가 되는 방식으로 정의를 했었죠?
- 따라서 z축으로 $\pi$ 만큼 rotation 실행
따라서 위의 식이 되고 $H=KR(z,\pi)$ 는 $KR$ 로 원래와 동일합니다.
순서를 정리해보자
1. Linear system 만들기!

- $a_{x_{i}}^{T}$ 와 $a_{y_{i}}^{T}$ 는 모든 observation에 의해 얻을 수 있음
2. SVD를 풀고 V의 마지막 column을 solution으로 선택하기!
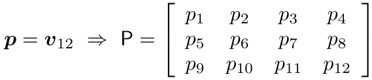
3. 만약 각각의 파라미터가 필요하다면 구하기!
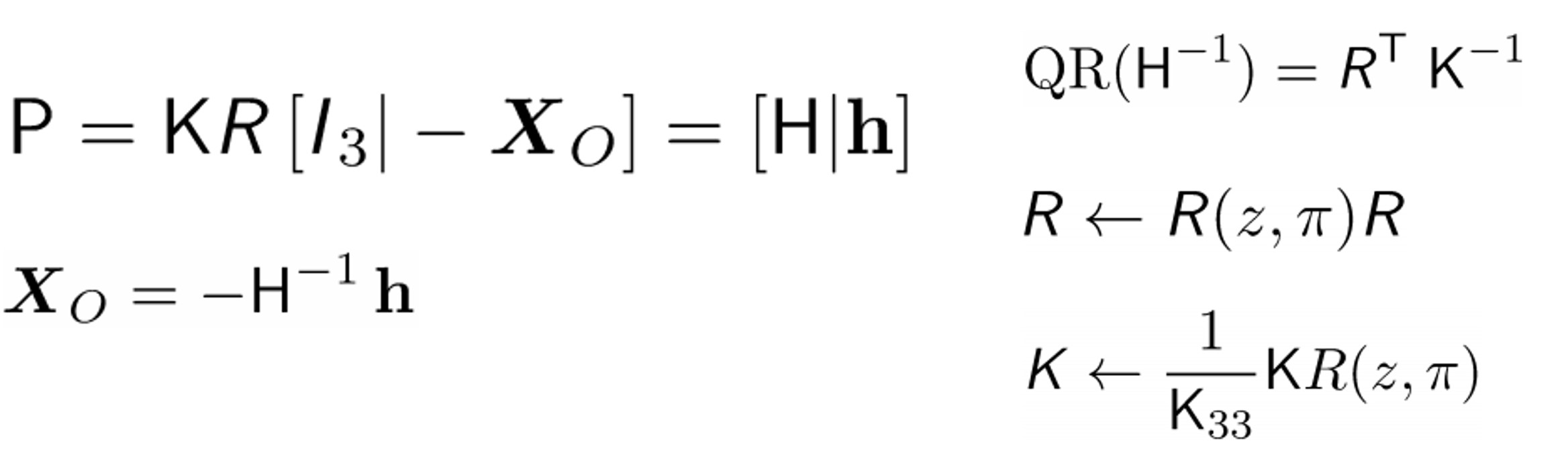
요약
Discussion
- $P$ $\leftrightarrow$ $(K, R, X_{O})$
- Control Point 가 평면에 존재하는 경우 solution이 불안정
- 초기값이 필요하지 않지만 불확실성을 고려하지 않은 점 존재
Summary
- DLT는 camera의 intrinsic과 extrinsic parameter를 estimate
- 최소 6개의 3D control point 를 알아야하는 전제 조건 존재
- Direct Solution (no initial guess)
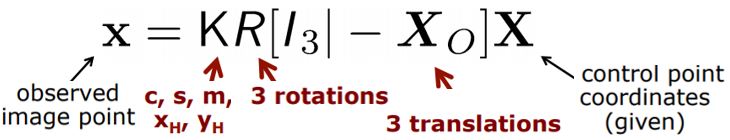

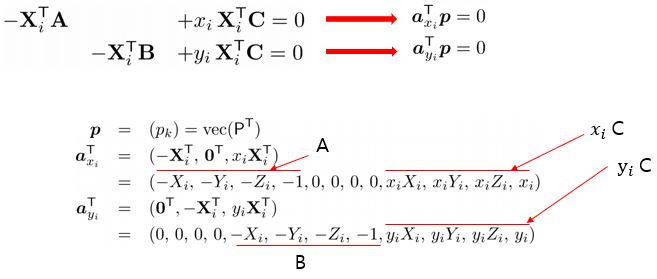

Leave a comment