Direct Solution for Estimating Fundamental & Essential Matrix - Camera Calibration (Photogrammetry)
Updated:
Direct Solution for Estimating Fundamental & Essential Matrix - Camera Calibration 공부하기
본 포스팅은 Cyrill Stachniss 교수님의 강의를 바탕으로 작성하였습니다.
강의 출처 : https://www.youtube.com/watch?v=zX5NeY-GTO0&list=PLgnQpQtFTOGRYjqjdZxTEQPZuFHQa7O7Y&index=46
수식 issue가 있어서 Cyrill Stachniss 교수님의 강의자료를 수정 후 올립니다.
Direct Solution for Estimating Fundamental & Essential Matrix
주제 : 내,외부 파라미터 없이 F와 E matrix를 구해보자!
오늘은 카메라의 intrinsic, extrinsic parameter 없이 아래를 구하는 것입니다.
- corresponding point가 주어질 때, fundamental matrix 구하기
- corresponding point가 주어질 때, essential matrix 구하기
- essential matrix가 주어질 때, Rotation matrix와 basis 구하기
눈치채신 분들은 아시겠지만 이번에 우리가 알고 있는 것은 이미지 내의 point pair입니다(위에서는 corresponding point라고 언급을 했었죠). 포스팅의 순서는 Fundamental matrix를 먼저 구해본 후 유사하게 Essential matrix를 구해보겠습니다.
Computing the Fundamental Matrix Given Corresponding Points
먼저 fundamental matrix F와 해당하는 coplanarity constraint는 다음과 같이 구성됩니다. 자세한 내용은 이전의 포스팅을 참고하시면 됩니다.

이전 포스팅에서는 Projection matrix P를 통해 K(Calibration matrix)와 R(Rotation matrix)를 구하고 를 얻었지만 본 포스팅은 이러한 정보가 없다고 가정한다는 차이가 있으니 유의하시길 바랍니다!
그러면 문제를 공식화해서 직관적으로 바라보도록 해봅시다.
- Given : N개의 corresponding point ( $(x’,y’){n}, (x’‘,y’‘){n}$ with $n = 1, … , N$)
- Wanted : fundamental matrix F
- 각 point마다 coplanarity constraint를 가지고 있음
- $x’{n}^{T}Fx’‘{n} = 0$ , $n=1,…,N$
즉 각 corresponding point에 대해 아래ㅢ 식을 가지고 있습니다.
- $x’{n}^{T}Fx’‘{n} = 0$ , $n=1,…,N$
이제 이 문제를 풀기 위해 어떻게 접근을 해야할까요? 가장 쉬운 방법은 Linear 방식으로 해결하는 것인데요. 기존에 포스팅했었던 DLT처럼 matrix를 구하고 vector로 변환후 구했던 방식을 여기서 다시 적용하면 되겠습니다. 이 Linear Dependency는 아래와 같습니다.

이 우측의 식을 $a_{n}^{T}$ 와 $f$ 로 정의한 후 Kronecker Product를 사용하여 아래와 같이 정의합니다. Kronecker Product에 대한 내용은 여기서 다루지 않겠습니다.
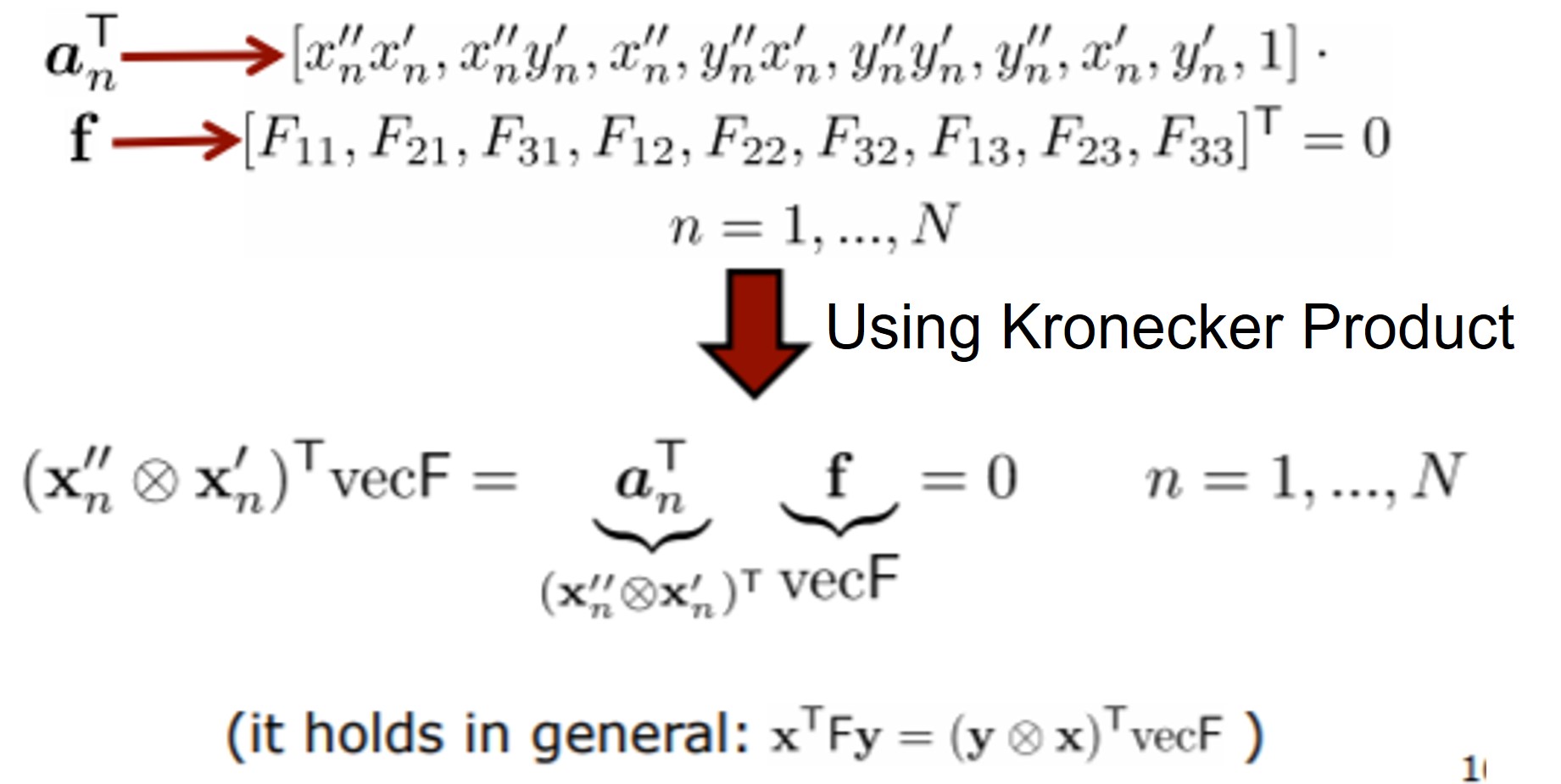
이제 모든 포인트에 대해 이 linear system을 풀면 되겠습니다.

그렇다면 과연 몇 개의 point가 필요할까요?
- f는 9 dimension
- Matrix A의 rank는 최대 8
- 따라서 최소 8개의 corresponding point 필요!
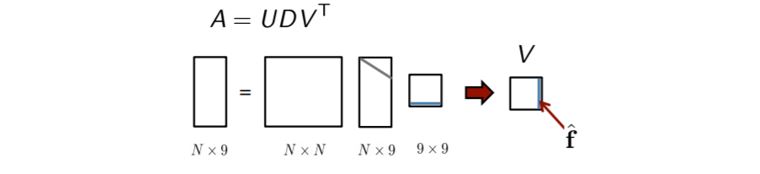
하지만 실제론 측정값이 noisy하기 때문에 8개 이상의 포인트를 사용을 하고 $\hat{f} \rightarrow \hat{F}$ 가 0이 아니라 minimize를 구하게 됩니다. 즉, 최솟값을 가지는 $\hat{f}$ 을 사용해서 $\hat{F}$ 을 구함
여기서 8-Point Algorithm $1^{st}$ TRY 를 하게 됩니다.
알고리즘은 위와 같습니다. Kronecker product를 사용한 후 SVD를 진행하게됩니다. 그 후 가장 작은 singular value를 가지는 singular vector를 선택하고 3x3으로 reshape한 것을 볼 수 있습니다. 하지만 여기서의 F는 rank가 2가 아닐 수 있지만 F의 rank를 2로 강제해야 합니다. 그 이유는 $\hat{F}$ 을 $F$ 에 가능한 근사하도록 해야하기 때문입니다. rank가 2여야 하는 이유는 여기 를 확인하면 더 좋을 것 같습니다. 이전 epipolar geometry와 연결되는 부분이 있습니다.
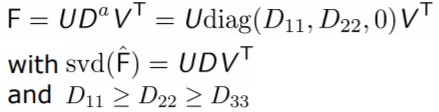
다시 돌아가 rank를 2가 되기 위해 8-Point Algorithm을 위와 같이 변경합니다. $\hat{F}$ 에 대해 second SVD를 하는 것을 확인할 수 있습니다. 이렇게 하면 최선의 근사치를 구할 수 있습니다. 변경된 알고리즘은 아래를 확인하시면 됩니다.
더 좋은 결과를 얻기 위한 방법들
- Normalization
- 해상도가 큰 이미지의 경우 좌표 값이 크게 되므로 0~1의 값을 가지도록 normalize (=scale 조절)
- Transform
- 모든 point 의 mass의 center가 (0,0)가 되도록 transform
즉, 새로운 coordinate 로 변환하는 T를 정의하게 됩니다. (T : Tx = $\hat{x}$ )
- 특징 : zero-centered 와 in [-1, 1]
따라서 새로운 coordinate에 대한 fundamental matrix $\hat{F}$ 를 아래와 같이 정의합니다. 이 $\hat{F}$ 는 위에 8-point 알고리즘에서 정의한 $\hat{F}$ 과 다르니 유의하시길 바랍니다.
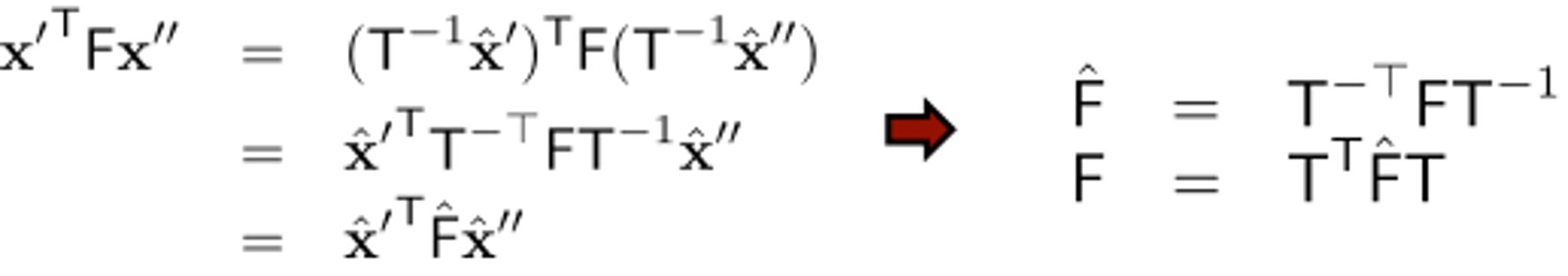
추가적으로 Singularity라는 것에 대해 강의에 설명을 해주셨습니다.
- Points on Plane
- 모든 corresponding point가 평면에 lie -> rank(A) < 8
- point들이 평면에 가까우면 수치적으로 불안정
- No Translation
- projection center가 동일하다면? $X_{O’} = X_{O’’}$
- 두 이미지 사이의 Translation이 0이 되고 그렇게 되면 fundamental matrix F 를 구할 수 없음
현재까지의 정리
- N pairs of corresponding points 에서 fundamental matrix F 구하기
- N>7일 때, homogeneous linear system을 푸는 것을 기반으로 한 Direct Solution 하기 (= 8-Point Algorithm)
- iterative 없이 바로 F를 구할 수 있음
동일하게 Essential matrix E를 구해보자!
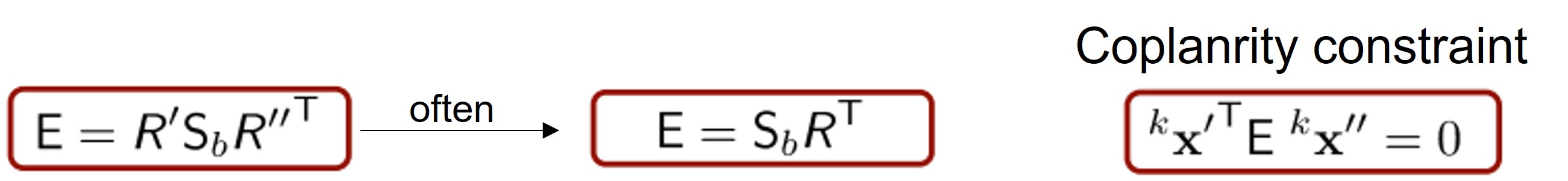
위는 E와 해당 제약 조건입니다. E의 경우 첫 번째 카메라의 rotation을 기준으로 잡기 때문에 가운데처럼 R’을 제외하고 표현하기도 합니다.
이제 원래 목표로 돌아가 구해보겠습니다. F를 구했으니 유사하고 더 쉽게 구할 수 있겠죠? 각 point 에 대해 아래와 같이 coplanarity constraint가 존재하겠고, E를 구하는 것은 F와 비슷합니다.
그렇다면 고려해야하는 제약 조건은 무엇일까요?? Fundamental matrix는 rank를 2로 강제를 했었죠? F를 svd를 진행하면 다음과 같았습니다. $F = UDV^{T} = U\begin{bmatrix}
D_{11} & 0 & 0
0 & D_{22} & 0
0 & 0 & 0
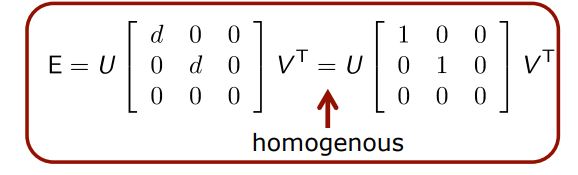
\end{bmatrix}V^{T}$ . Essential matrix의 경우 0이 아닌 singular value가 모두 동일한 값을 가지게 됩니다.
Essential matrix에 대한 8-Point Algorithm은 아래와 같습니다.
이렇게 E를 구하게 됩니다. F와 마찬가지로 normalize와 transform을 한다면 더 좋은 결과를 얻을 수 있게 됩니다. 새롭게 정의된 coordinate로의 변환을 T로 정의하면 아래와 같고 해당 T로 $\hat{E}$를 표현할 수 있습니다.
5-Point Algorithm
Essential matrix E의 property는 아래와 같습니다.
- homogeneous
- Singular $| E |$ = 0 (determinant is zero)
- Two identical non-zero singular values
- As a result of the skew-sym. Matrix : $2EE^{T} - tr(EE^{T})E = \underset{3\mathrm{x}3}{0}$
- Essential Mat.은 5 DoF를 가지기 때문에 7 DoF를 가지는 랑 달리 8-Point algorithm 말고 더 줄일 수 있다.
5-Point algorithm에 대한 간략한 설명은 아래와 같습니다.
- 2003/2004 년도에 제안됨
- 종종 RANSAC과 같이 사용됨
- Calibrated camera에서 Relative Orientation을 계산할 때 사용
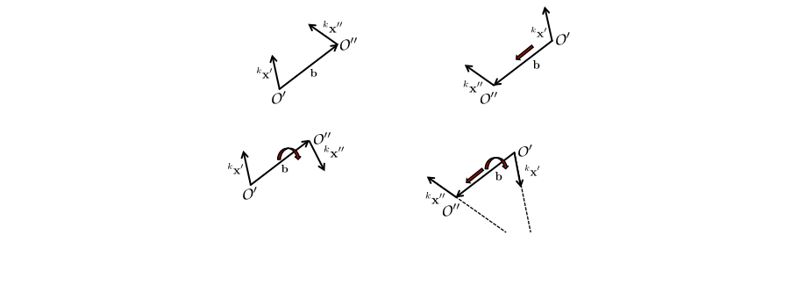
3번째에서 말한 Relative orientation 파라미터를 계산할 때에 대해 알아보겠습니다. E가 주어질 때 Basis와 Rotation을 계산할 수 있다는 것입니다($E\rightarrow S_{B},R$). 하지만 과연 unique한 solution이 있을까요? 물리적으로는 하나의 해가 있지만 대수적으로는 아래처럼 4개가 존재합니다.
basis에 -1을 곱한 것과 방향을 반대로 뒤집으면 4개가 나올 수 있습니다. 여기서 물리적으로 가능한 해는 좌측 위가 되겠습니다. 카메라가 모두 정면을 바라보는 방향이니까요. 하지만 우리가 E를 통해 해를 구했을 때 이게 물리적으로 가능한 해이다!를 아는 방법이 필요하겠죠? 이제 알아보겠습니다.
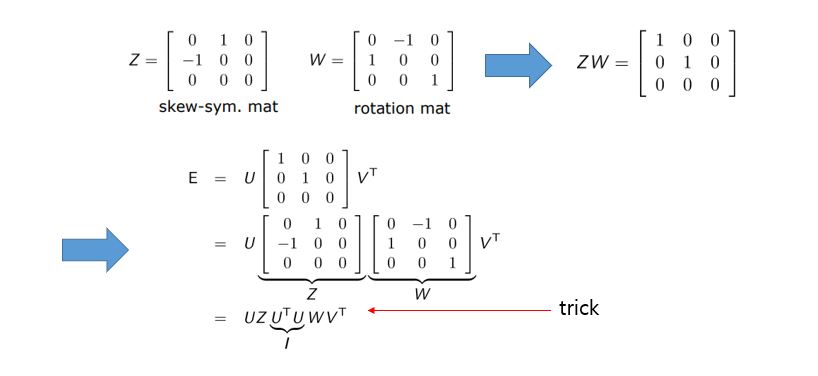
Algebraic solution에 대해 구해보겠습니다. hartley와 Zisserman에 의해 구해졌다고 합니다. 우리가 아는 것은 E를 svd로 했을 때 U와 $V^{T}$는 rotation matrices이고 가운데는 마지막 원소가 0인 matrix입니다. 여기서 새로운 Z와 W를 아래와 같이 정의합니다. ZW는 $\hat{D}$가 됩니다. 따라서 분해할 수 있고 마지막 줄에는 trick을 사용하여 I = $U^{T}U$ 를 넣습니다.
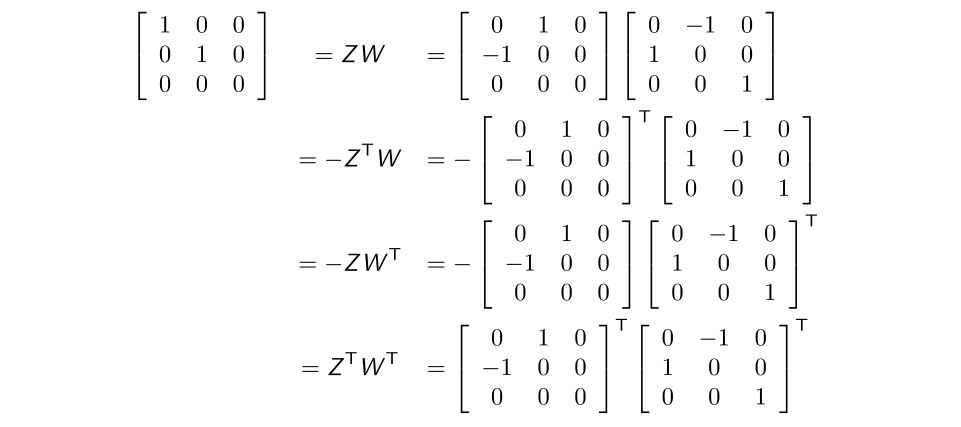
또한 Z와 W로 $\hat{D}$ 를 표현하는 방법은 4가지입니다.
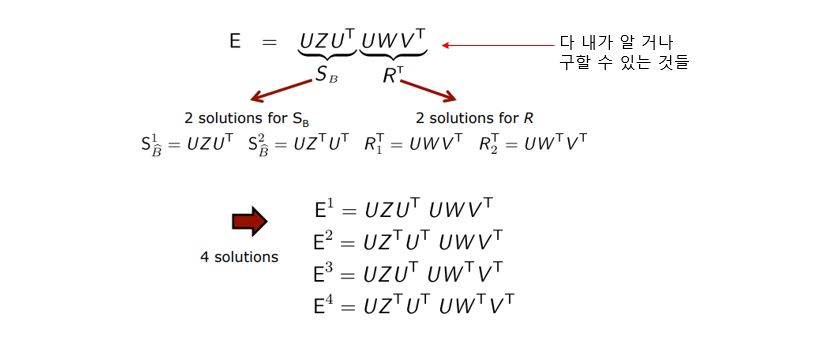
그렇다면 총 4개의 solution이 나올 수 있겠습니다.
정리해보겠습니다.
- E의 SVD를 계산
- U와 V를 normalize : U = U $| U |$ , V = V $| V |$
- 4개의 solution을 계산 :
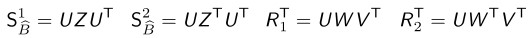
- test를 해서 카메라의 방향을 확인(카메라의 방향이 앞인지 뒤인지)
- 물리적(physically)하게 올바른 것을 return하여 해 선택
Summary
전체적인 요약은 아래와 같습니다.
- Image data에서 relative orientation을 계산하는 알고리즘
- scene에 대한 지식 없이 image pair 값만 가지고 계산하였음
- scale을 제외하고 camera motion을 estimate하는 것이 가능
- Direct solutions
- F from N>7 points (“8-Point Algorithm”)
- E from N>7 points (“8-Point Algorithm”)
- E from N=5 points (“Nister’s 5-Point Algorithm”)
- Direct solutions
- 초기값이 필요하지는 않지만 불확실성을 고려하면 최적의 해는 아님
- Extracting $S_{B}$ , $R$ from E
- RANSAC으로 outlier 제거 후 inlier만 사용하기도 함
- Direct solution & RANSAC은 iterative solution을 위한 초기값 제공
- inlier point만을 기준으로 least squares를 사용하여 subsequent refinement





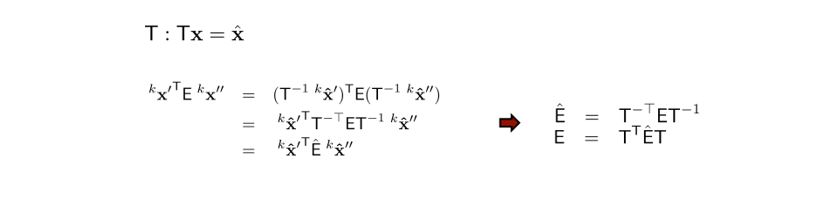
Leave a comment