Epipolar Geometry - Camera Calibration (Photogrammetry)

Epipolar Geometry - Camera Calibration 공부하기

본 포스팅은 Cyrill Stachniss 교수님의 강의를 바탕으로 작성하였습니다.

강의 출처 : https://www.youtube.com/watch?v=cLeF-KNHgwU&list=PLgnQpQtFTOGRYjqjdZxTEQPZuFHQa7O7Y&index=43

수식 issue가 있어서 Cyrill Stachniss 교수님의 강의자료를 수정 후 올립니다.

Epipolar Geometry

주제 : Epipolar Geometry에 대해 공부해보자!

coplanarity Constraint의 특징은 아래와 같습니다.

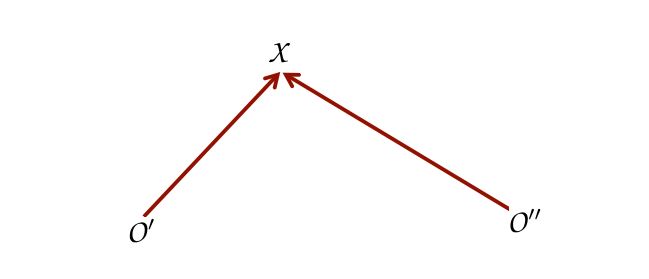
• Two corresponding rays의 intersection
• Rays는 3D의 평면에 lie

Epipolar Geometry의 Motivation

• Given : First iamge에서 볼 수 있는 point X’
• Find : Second image에서 Given으로 주어진 X’와 같은 corresponding point X” 찾기

Epipolar Geometry

Epipolar Geometry는 일반적으로 image pair의 기하학적 관계를 설명하는 데 사용됩니다. Corresponding point의 prediction과 efficient search를 가능하게 합니다. staright-line preserving mapping이 주어지면, search space를 2D에서 1D로 줄일 수 있기 때문에 더 빠르고 data를 연결할 때 mistake를 줄일 수 있게 됩니다.

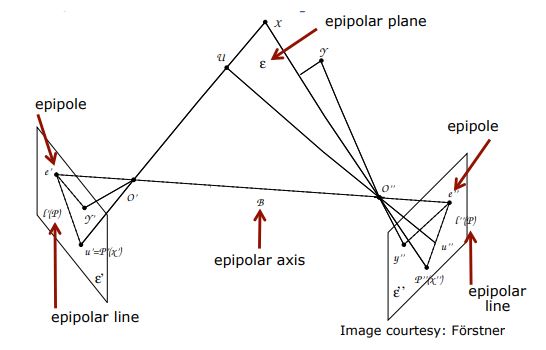
Important Elements

• Epipolar axis : $B$ = (O’O”) , 두 projection center를 연결하는 선
• Epipolar plane : $\varepsilon $ , O’X’, O”X”를 연결하는 plane
• Epipole : $e’$ = (O”)’, $e’’$ = (O’)” , 다른 projection center로부터 투영된 점
• Epipolar line : $l’(X)$ = (O”X)’, $l’‘(X)$ = (O’X)” , epipolar plane과 image plane의 intersection

epipolar axis라고 부르는 이유는 world coordinate X가 어디에 있든 epipolar axis를 축으로 epipolar plane이 움직이기 때문입니다.

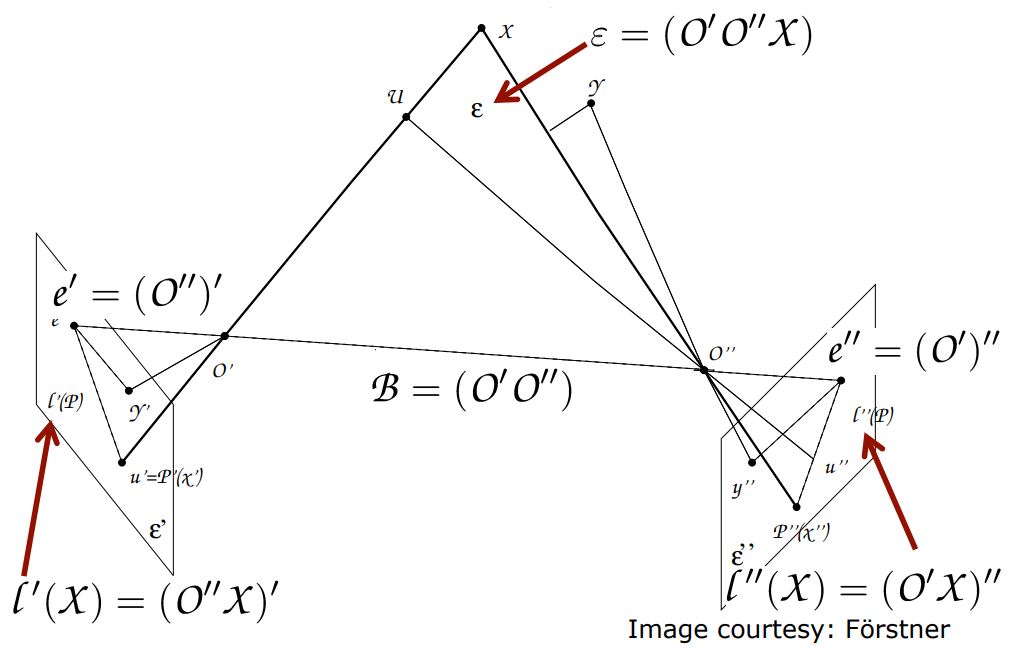
In the epipolar plane..

Distortion-free lens를 사용하면,

• the projection centers O’, O”
• the point X
• the epipolar lines $l’(X)$ , $l’‘(X)$
• the epioples $e’$ , $e’’$
• the image points $X’$ , $X’’$

위 모두가 epipolar plane에 lie하게 됩니다. 그렇기 때문에 다른 image에서 corresponding point의 위치를 predict하는 것을 단순화 시킬 수 있습니다.

Predicting the Location of Corresponding Points

• Task : X’가 주어졌을 때 X”의 위치를 predict
• Epipolar plane throught $\varepsilon$ = (O’O”X)
• Epipolar plane과 second image plane $\varepsilon ‘’$ 의 intersection은 epipolar line $l’‘(X)$ 생성
• Corresponding point X”는 epipolar line $l’‘(X)$ 에 lie
  • Reduces the search space from 2D to 1D

큰 틀은 이제 배웠습니다. 그러면 실제로 어떻게 구하는지만 알면 됩니다! 먼저 정답을 공개하면 Projection matrices와 fundamental matrix 기반으로 계산한다고 보시면 됩니다.

Computing the Key Elements of the Epipolar Geometry

하나씩 구해봅시다. 먼저 Epipolar axis의 direction은 projection center로 계산이 됩니다. 하지만 방향만 알고 길이는 모른다는 것을 잊으시면 안됩니다. 다음과 같이 표현할 수 있습니다. $b$ = $X_{O’’}$ - $X_{O}$

Epipolar line에 대해 생각해봅시다. image point는 epipolar line에 lie하고 있는 것을 알 수 있습니다. 즉 $x’^{T}l’$ = 0입니다. 이 식과 추가적으로 두 포인트 X’, X”의 coplanarity constraint를 이용하면 아래와 같습니다.

반대도 가능하며, 우리가 예측한 prediction이 1D space이고 이 line을 따라 search하면 다른 해당 점을 찾을 수 있겠습니다.

Epipole은 다른 image의 projection center를 projection하여 얻을 수 있습니다. 식은 아래와 같습니다.

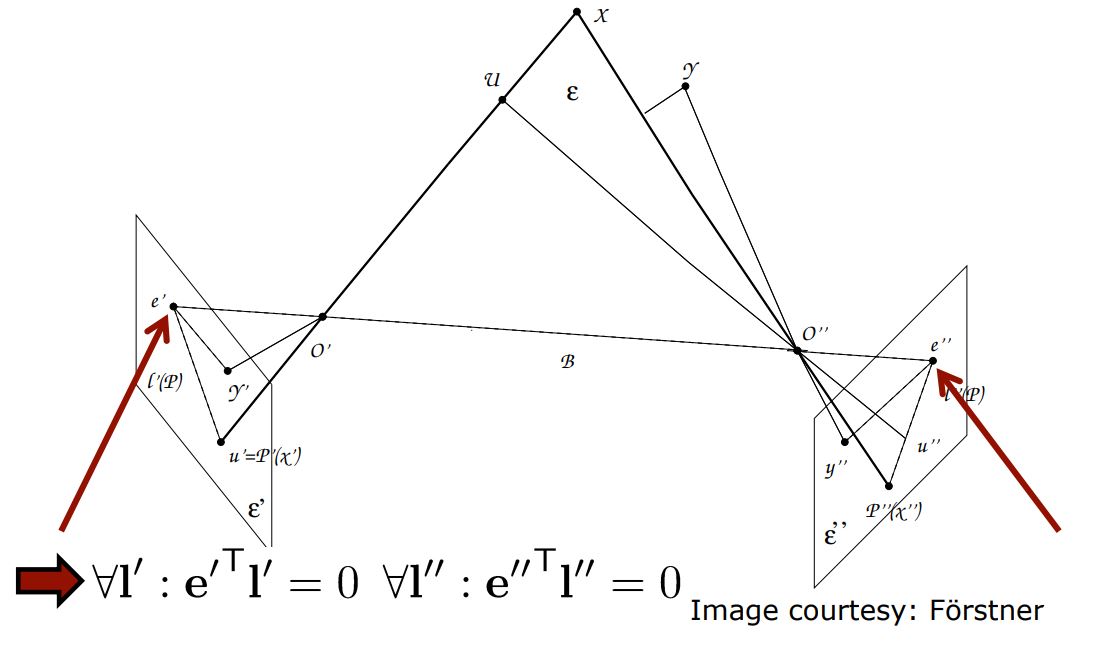
Epipole is the intersection of All Epipolar Lines in an image

위 그림은 존재할 수 있는 모든 epipolar line에 대해 위 식을 만족하는 것을 표현합니다. 즉, epipole은 모든 epipolar line에 intersection합니다. 이 성질과 이전에 구한 $l’$ = Fx”를 combine하여 $e’^{T}Fx’’$ = 0을 얻습니다. 이 식에서 x”는 모든 값에 대해 epipolar line에 속하므로 $F^{T}$ 의 null space를 구한다면 e’를 구할 수 있게 됩니다. 유사하게 두 번째 epipole에 대해서도 구할 수 있게 됩니다.