Relative Orientation Fundamental & Essential Matrix - Camera Calibration (Photogrammetry)
Updated:
Relative Orientation Fundamental & Essential Matrix - Camera Calibration 공부하기
본 포스팅은 Cyrill Stachniss 교수님의 강의를 바탕으로 작성하였습니다.
강의 출처 : https://www.youtube.com/watch?v=gYYumFSDsvA&list=PLgnQpQtFTOGRYjqjdZxTEQPZuFHQa7O7Y&index=42
수식 issue가 있어서 Cyrill Stachniss 교수님의 강의자료를 수정 후 올립니다.
Relative Orientation Fundamental & Essential Matrix
주제 : Relative Orientation에 대해 공부해보자!
Camera Pair는 크게 2가지로 분류할 수 있습니다. 첫 번째는 스테레오 카메라로 한 카메라에 2개의 렌즈가 달려있는 경우이며, 두 번째는 한 카메라에 대해 이동시켜 촬영하는 경우가 있겠습니다. 이번 포스팅의 경우 두 번째 경우를 가정한다는 점 유의하시길 바랍니다.
그렇다면 Orientation이란 무엇일까요?
- Mapping과 관련된 파라미터
- Camera pair의 orientation은 각 camera에 대한 독립적인 orientation을 사용하여 설명 가능
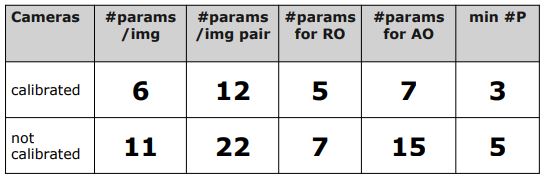
- Calibrated camera : 12 parameters
- Uncalibrated camera : 22 parameters
질문 : “Scene에 대한 정보 없이 camera motion을 estimate할 수 있을까?”
- 이전에 배운 카메라의 파라미터를 구하는 방법은 control point를 알고있다고 가정함
- 2개의 scene에서 camera motion을 설명할 수 있는 방법?
- 구할 수 있는 파라미터와 구할 수 없는 파라미터 존재
- 예 : 단일 이미지에서는 scaling 정보를 얻을 수 없음 (사전 정보 필요)
구할 수 있는 파라미터와 구할 수 없는 파라미터??
- 카메라가 2대여도 하나가 calibrated 상태이면 상대적인 orientation을 estimate 가능함
- 카메라가 relative transformation을 유지하는 경우
- scale처럼 global translation & rotation 얻기 불가능 함
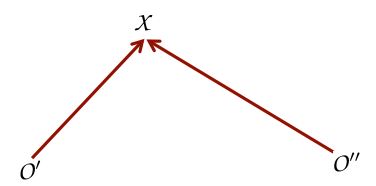
위 그림처럼 scale 정보를 알 수 없습니다.
즉, scene에 대해 알지 못한다면 2번째 카메라가 어디에 있는지 설명이 불가능합니다. 전체 규모를 측정할 수 없음을 의미합니다. 다시 돌아와서 calibrated 카메라의 경우 12개의 파라미터가 존재하는데 그 중 7개(translation, rotation, sclae)를 알 수 없으며, 5개(1번 카메라를 기준으로 2번 카메라의 상대적인 위치)의 파라미터를 알 수 있습니다.
그렇다면 결과적으로 구할 수 있는 파라미터는 아래와 같습니다.
- 첫 번째 카메라와 관련하여 두 번째 카메라의 Rotation Matrix (3 parameters)
- Projection center를 연결하는 direction B (2 parameters)
- B의 길이는 scale 장변에 대한 지식이 없기 때문에 구할 수 없음
Calibrated camera에서..
orientation에서 2개의 calibrated camera에 대해 2 x 6 = 12 parameter가 필요합니다. 여기서 추가적인 정보 없이, 5개의 파라미터를 얻을 수 있죠 (7개는 위에 말했던 trans, rot, scale입니다).
Uncalibrated camera에서..
projective transform은 15개의 파라미터를 가지기 때문에 2개의 이미지에서 7개(=22-15)의 파라미터만을 얻을 수 있습니다. 만약 relative가 아닌 absolute orientation을 얻고싶다면 최소 3D point 5개를 알아야 됩니다.
Relative Orientation Summary
- RO = relative orientation
- AO = absolute orientation
- min #P = min. number of control points
이번에는 RO를 구하는 것에 집중해보자!
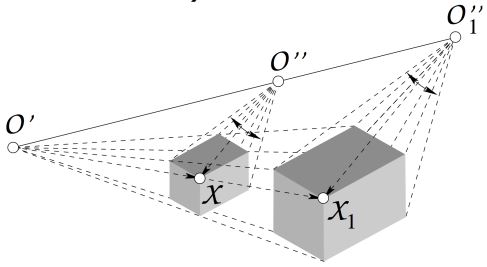
일단 Uncalibrated cameara로 가정을 하겠습니다. scene에 대한 정보 없이 구할 수 있는 파라미터는 무엇일까요? 우선 아래 그림에서의 특징에 대한 가정을 설명하자면 scene에 대한 정보가 없으며, projectino orientation (=noise X) 의 X 지점이 정확히 같은 지점이고, 2개의 ray가 교차(intersection)한다는 것입니다. 이렇게 된다면, 두 벡터 내에 있는 평면이 존재하게 되고, 두 projection center를 지나는 벡터도 같은 3D 평면에 존재하게 되겠습니다. 그 결과, uncalibrated camera의 coplanarity constraint 는 아래와 같습니다.
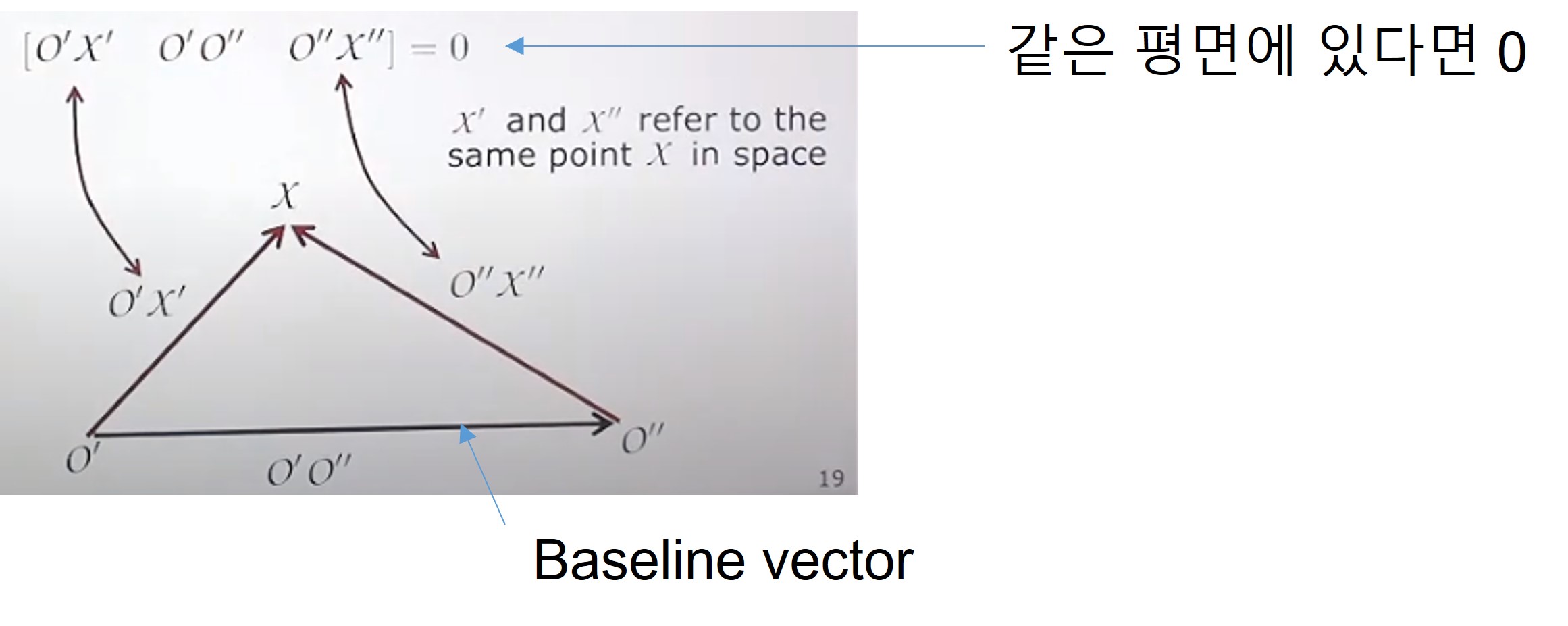
Scalar Triple Product [ $\cdot$ , $\cdot$ , $\cdot$ ]
위 그림에서 나온 연산자에 대해 간단히 설명드리겠습니다. 입력으로 3개의 vector를 취하는 연산자로, 기본적으로 계산하는 것은 평면육면체의 volume이 되겠습니다. [A,B,C] = (AXB) $\cdot$ C 로 A와 B를 외적하면 수직인 방향이고 그것과 C와 내적한다고 풀어 생각하시면 됩니다. 따라서 이 결과값이 0이라면 vector가 one plane에 있는것이 되겠습니다.
돌아와서 이 속성을 카메라에 대해 무엇을 할 수 있는지를 생각해보면, 카메라가 3D point를 projection 한다는 것입니다.
먼저 벡터 O’X’와 O”X”는 iamge coordinate x’,x”에서 파생될 수 있습니다. 따라서 x’=P’X, x”=P”X이며, projection matrix는 P’=K’R’[ $I_{3} |$ - $X_{O’} $ ], P”=K”R”[ $I_{3} |$ - $X_{O’’} $ ]입니다. 그리고 O’X’와 O”X”는 카메라의 calibrated matrix를 고려하여 계산할 수 있는 vector입니다.
Direction to a Point
O’X’와 O”X”를 먼저 구해보겠습니다. 이 두 벡터의 normalized direction과 normalized projection은 아래와 같습니다. ‘을 “로 바꾸면 3번째 image coordinate입니다.
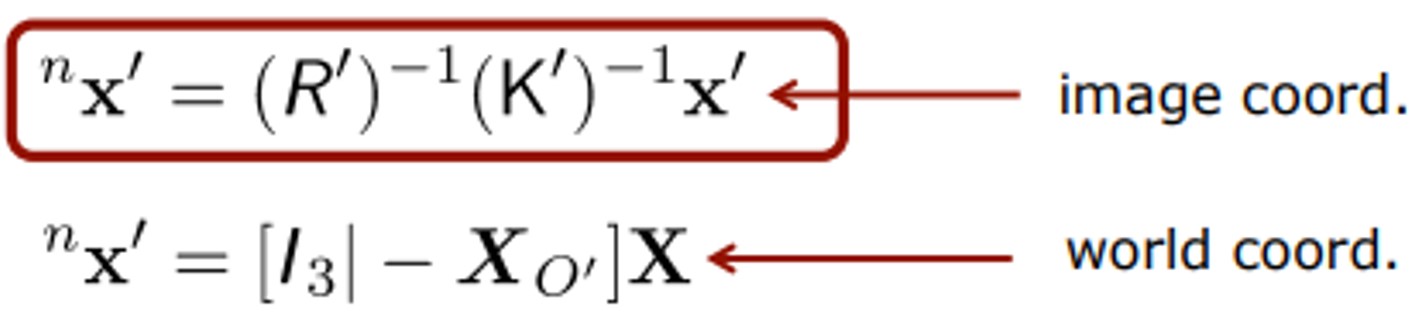
Base Vector
Base Vector O’O”는 projection center의 차로 바로 얻을 수 있습니다. 식은 아래와 같습니다.
그렇다면 이전 식에 위에서 구한 것들을 대입할 수 있게 됩니다. coplanarity constraint [O’X’ O’O” O”X”] = 0을 다시 쓰면 아래와 같습니다.
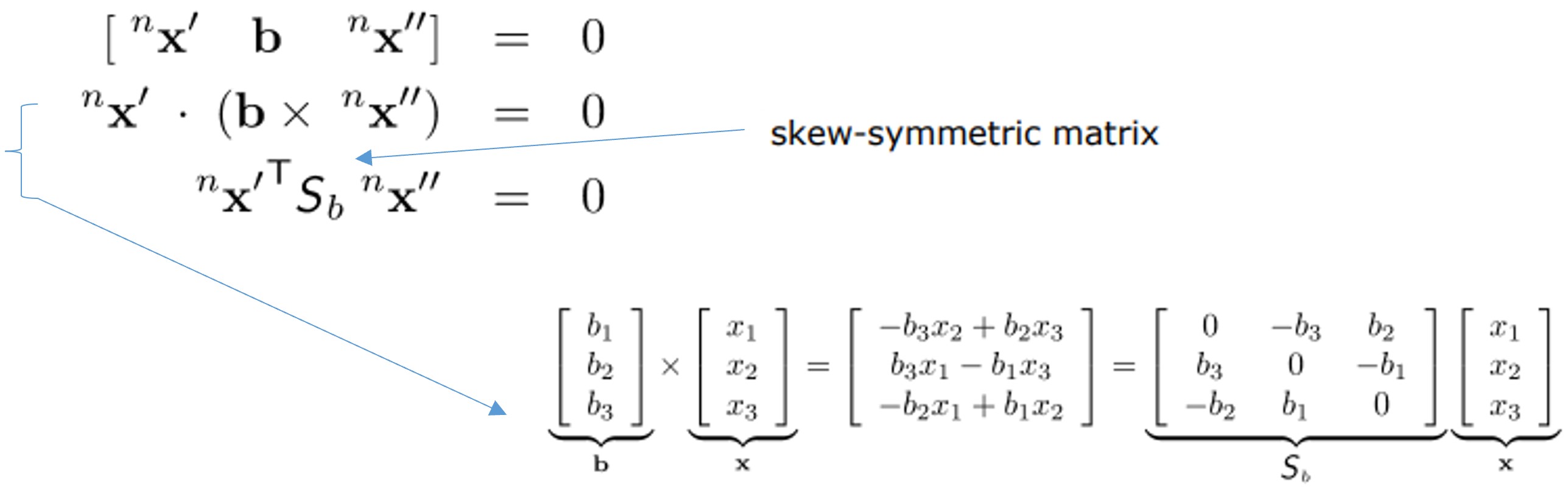
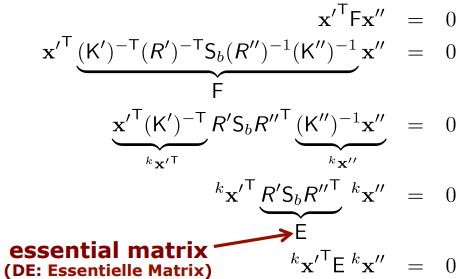
두 번째 줄에서 세 번째 줄로 넘어가는 건 외적을 내적으로 표현한 것이고 그 결과 가운데 $S_{b}$ 가 skew-symmetric matrix가 됩니다. 마지막 식을 위에서 구한 것들로 채우면 완성하게 됩니다.
이 F를 fundamental matrix라고 부르며 uncalibrated camera일 때의 경우입니다. 이 matrix는 하나의 respect하는 camera의 RO에 대해 estimate할 수 있는 모든 파라미터를 설명하고, 7 DoF(=22-15)를 가집니다. 결과적으로, $x’^{T}Fx’’$ = 0을 만족시키는 F라고 생각하시면 됩니다.
그러면 이제 “2개의 projection matrix가 있으면 F를 구할 수 있는가”를 생각해봅시다.
Fundamental matrix from the camera projectino matrices
P’, P”는 모두 3x4 matrix이죠. 결과적으로 이를 통해 F를 구할 수 있습니다. 구하는 방법은 다음과 같습니다.
P를 3x3 matrix와 3x1 vector로 분해하여 아래와 같이 표현합니다.
위 식에서 projection center를 구할 수 있습니다. (2번 카메라에서도 동일하게 수행 가능)
Baseline B는 2개의 projection center의 차이로 주어지므로 아래와 같겠습니다.
이렇게 구한 두 식으로 F를 계산할 수 있습니다!
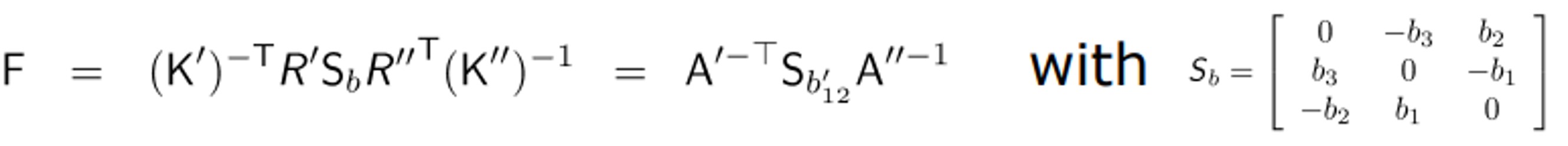
Essential matrix(for calibrated cameras)
대부분의 photogrammetric system은 calibrated camera에 의존합니다. 여기서는 2대의 카메라가 동일한 calibration matrix를 가진다고 가정합니다. 또한 distortion이 없고, 다른 imaging error가 없다고 가정합니다.
Calibrated camera의 경우 coplanarity constraint는 더 단순합니다. calibration matrix를 기반으로 direction을 다시 쓰면 아래와 같습니다.
Mapping을 단순화 가능하게 해서 relation results는 아래와 같습니다.
그렇다면 아까 uncalibrated camera에서 정의했던 F를 변경할 수 있습니다. 아래처럼요.
우리는 이 E를 Essential Matrix라고 부르며 특징은 아래와 같습니다.
- 5 DoF(=15-7), scene 정보 없이 calibrated camera의 relative moving에서 estimate
- calibrated camera에서 image pair의 relative orientation을 결정하는 5 parameter 존재
- 4(=9-5) constraints 존재 (3x3 matrix 원소 중)
Summary
오늘 포스팅에서 공부한 것들은 아래와 같습니다. 아래 키워드에 대해 잘 이해가 가지 않으셨다면 추가적인 자료들을 보시는 것을 권장드립니다..
- Parameters of image pairs
- Relative orientation
- Fundamental matrix F
- coplanarity constraint $x’^{T}Fx’’$ = 0
- Essential matrix E
- coplanarity constraint $^{k}x’^{T}E^{k}x’’$ = 0
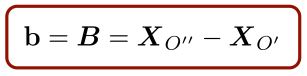
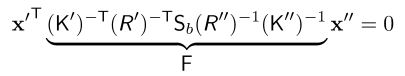
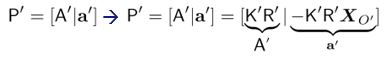
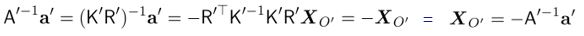
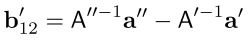

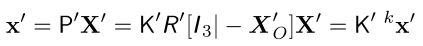
Leave a comment