Zhang’s Method - Camera Calibration (Photogrammetry)

Zhang’s Method - Camera Calibration 공부하기

본 포스팅은 Cyrill Stachniss 교수님의 강의를 바탕으로 작성하였습니다.

강의 출처 : https://www.youtube.com/watch?v=-9He7Nu3u8s&list=PLgnQpQtFTOGRYjqjdZxTEQPZuFHQa7O7Y&index=38

수식 issue가 있어서 Cyrill Stachniss 교수님의 강의자료를 수정 후 올립니다.

Zhang’s Method

주제 : 카메라의 내부 파라미터 구하기

• 가정 : DLT에 필요한 3D control point 좌표를 알고 있음
• Zhang’s method란?
  • checkerboard를 이용하는 방법
  • 20년 전에 개발됨

오늘의 주제는 카메라의 내부 파라미터를 구하는 것입니다. 이번 포스팅에서는 외부 파라미터를 고려하지 않고 내부 파라미터를 구하는 방법인 Zhang’s method에 대해 공부한 것을 공유하겠습니다. Zhang’s method란 checkerboard를 이용하며 알고 있는 3D point를 사용하는 것이 아닌 checkerboard 패턴을 사용하여 내부 파라미터를 구하는 방법이라고 이해하시면 될 것 같습니다.

2D checkerboard를 이용한 camera Calibration이라고 생각하시면 되며, checkerboard의 size와 structure를 알고 있으며 2D 패턴을 알 수 있다고 생각하시면 됩니다.

Camera Calibration 을 위해 간단한 Trick 사용!

간단한 트릭을 사용합니다. 어떠한 트릭인지 알아보겠습니다. 먼저 트릭을 간단하게 설명해드리면 checkerboard의 코너를 world 좌표 시스템으로 설정을 하는 것입니다. 순서는 다음과 같습니다. 단순하게 먼저 corner detector를 통해서 checkerboard의 모든 코너를 검출합니다. 그렇게 되면 검출된 corner가 3D world에 있지만 어디에 있느지는 모르게 되겠죠. 여기서 이제 트릭을 사용하는 겁니다. 모든 이미지에 고유한 좌표계를 정의를 해버리는 겁니다! 모든 점이 바둑판 위에 있고, 3D world의 모든 좌표가 z=0을 가지게 말이죠. x, y 좌표의 경우 위에 설명한 checkerboard의 structure와 size를 알고 있기 때문에 알 수 있겠죠.

그렇게 되면 projection matrix를 아래와 같이 변경할 수 있게 됩니다. z=0이기 때문입니다.

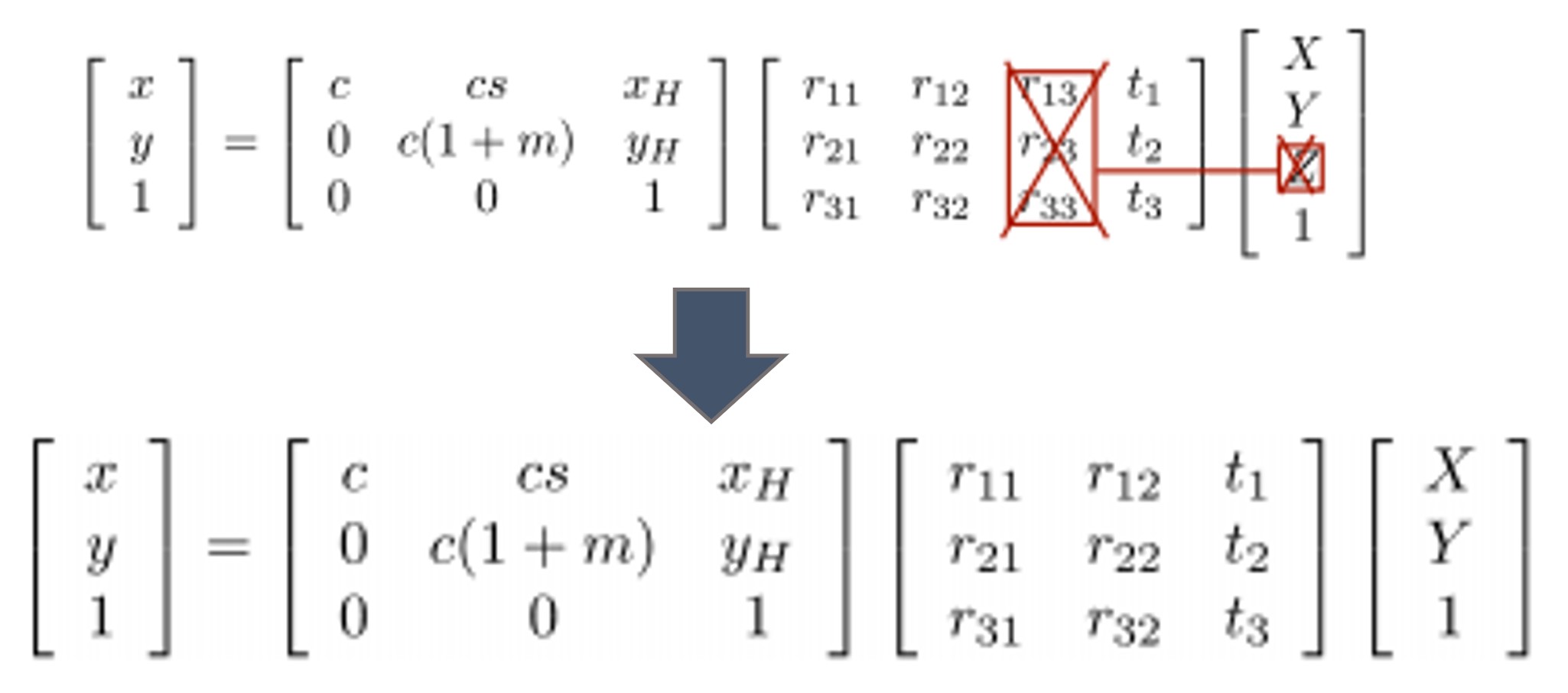
새롭게 H를 정의를 아래와 같이 하게 되면 한 개의 point를 정의하는 식을 세울 수 있게 됩니다.

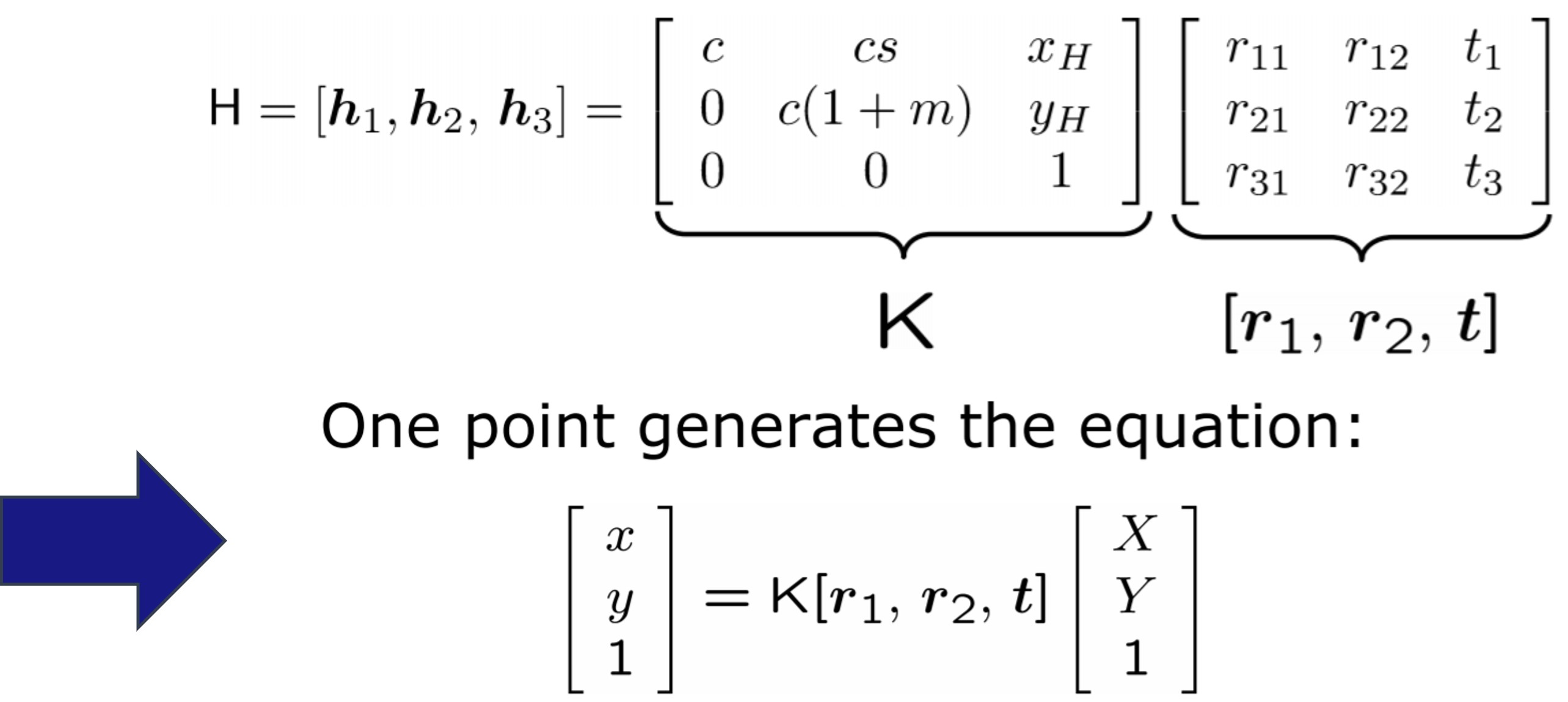
그렇게 되면 하나의 이미지에서 여러 개의 point에 대한 방정식은 아래와 같습니다.

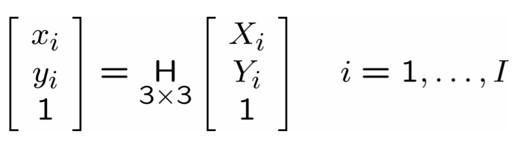
DLT와 유사하게 Estimation

이전에 배웠던 projection matrix는 3x4 matrix 였죠. 하지만 지금은 z=0이기 때문에 3x3 homogeneous matrix를 새롭게 estimate 해야 합니다. 그 이외의 나머지 부분은 동일하기 때문에 이전의 DLT로 camera calibration한 포스팅을 먼저 보고 본 포스팅을 읽으시는 것을 추천드립니다. 결과적으로 아래와 같이 되겠습니다. projection matrix의 경우는 12차원이었지만 지금은 9차원으로 변경된 것을 확인할 수 있습니다.

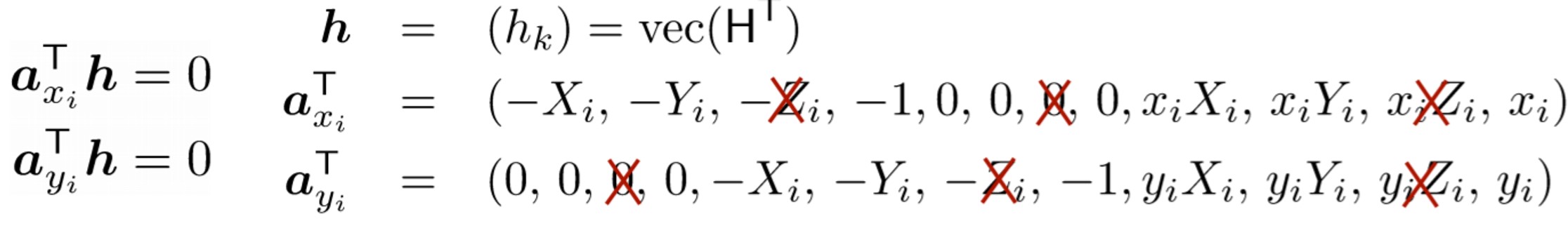
이제 DLT와 마찬가지로 SVD를 구해야 합니다. 그렇다면 H를 estimate하기 위해 몇 개의 point가 필요할까요? 8개의 DoF를 가지므로 최소 4개의 point가 필요합니다! (DLT의 경우 6개의 point가 필요했습니다.) 이렇게 H를 구하게 되면 H로부터 K를 구해야 합니다. DLT와 다른 점은 우측의 행렬이 더이상 Rotation Matrix가 아닌 것입니다! 즉, DLT에서처럼 QR Decomposition을 사용하지 못하게 됩니다..

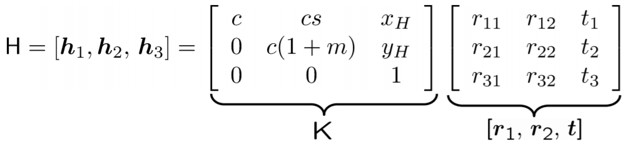
그러면 H를 어떻게 분해해야 할까요?? 먼저 우리가 원하는 것을 다시 볼 필요가 있습니다. H 중 K(=intrinsic parameters)를 구하고 싶습니다.

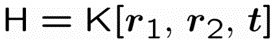
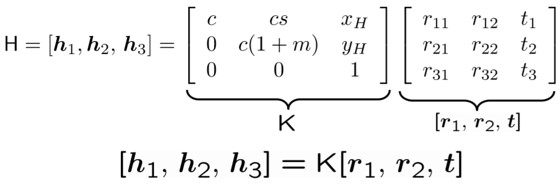
H에서 K를 계산하기

지금 헷갈리지 말아야할 것은 지금 하나의 이미지에서 계산중이라는 것입니다. 하나의 이미지에서 여러개의 포인트에 대해 SVD를 구했고 H까지 구한 것입니다. 그러면 이제 다시 K를 구해보겠습니다. 순서를 간단하게 적어보겠습니다.

• $K$ , $r_{1}$ , $r_{2}$ 에 대한 제약 조건 활용
• Matrix $B$ = $K^{-T}$ $K^{-1}$ 을 정의
• $B$ 를 구한 후 decompose

먼저 $K$ , $r_{1}$ , $r_{2}$ 에 대한 제약 조건을 활용해봅시다. $K$ 는 역행렬이 가능한 matrix이므로 양변에 $K^{-1}$ 을 곱합니다. 현재 H는 구해서 알고있는 값인 것을 유의하시길 바랍니다.

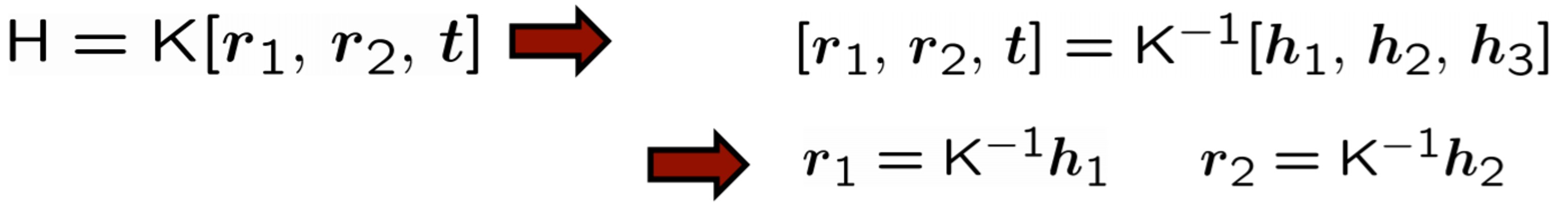
Rotation matrix $r_{1}$ , $r_{2}$ 는 orthonomal basis하다는 성질을 이용하여 제약조건을 만듭니다. 아래와 같습니다. 위는 orthonormal basis의 성질이며 아래가 그 성질을 이용하여 만든 제약 조건입니다.

식을 다시 가져와서 가운데 빨간색 밑줄친 부분을 $B$ 로 정의를 합니다. matrix $B$ 는 symmetric and positive 입니다.

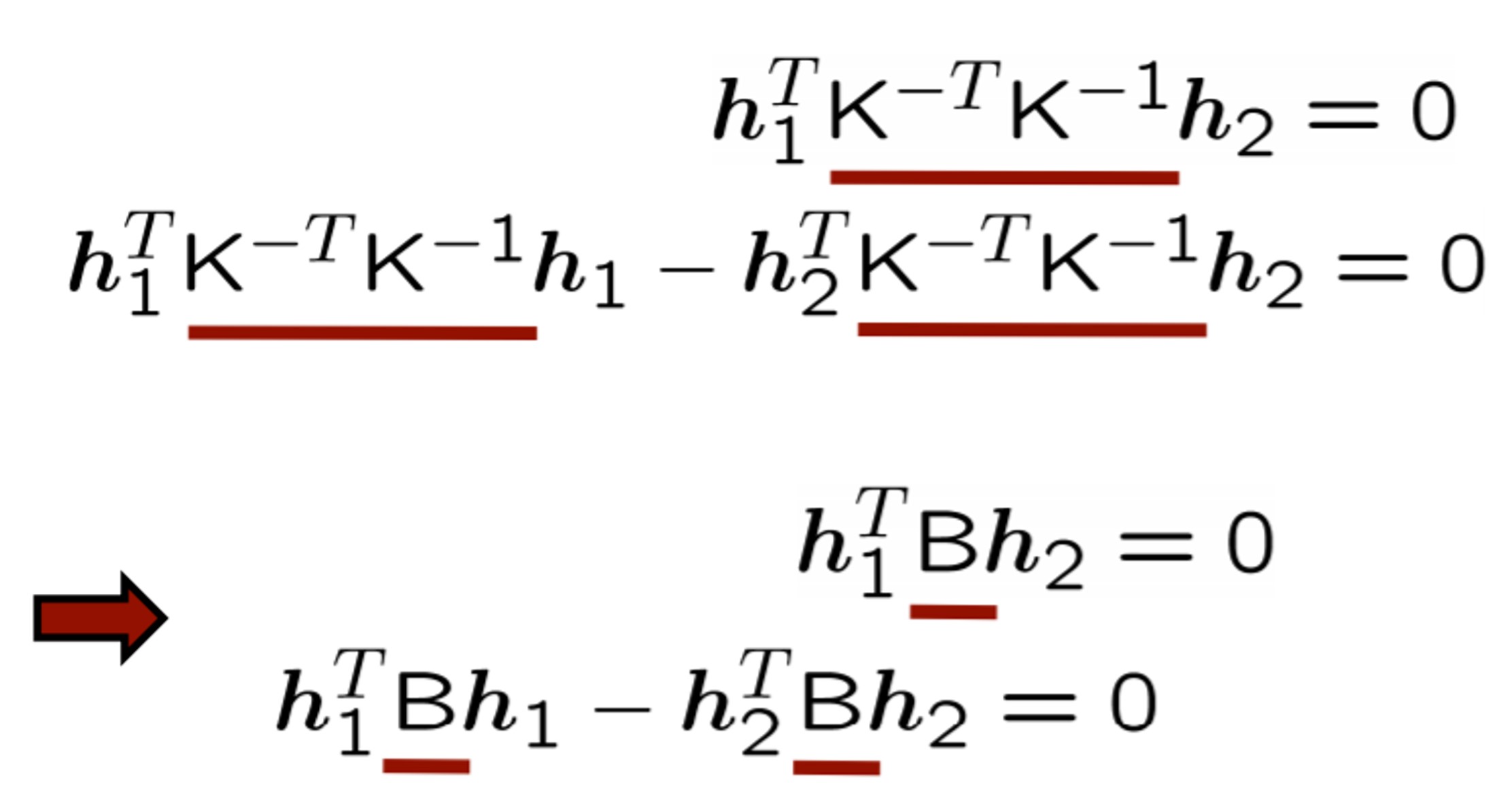
위 식을 보면 H로부터 나온 $h_{1}$ 과 $h_{2}$ 는 알고 있는(구한) 값이며, Cholesky decomposition으로 B를 분해할 수 있습니다. Cholesky decomposition이란 아래 그림처럼 어떠한 행렬 B가 있을 때, $AA^{T}$ 로 분해하는 decomposition입니다.

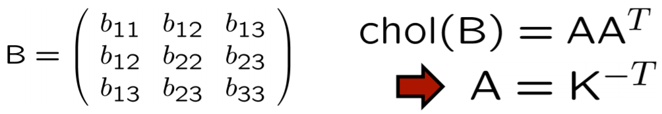
그러면 우리가 B를 알고 있다면 K를 계산하여 얻을 수 있습니다. 이제 B를 구해야겠죠. 그럼 이제 B가 뭔지 생각해봅시다. $h_{1}$ , $h_{2}$ , $B$ 가 있는 식에서 우리가 알 수 있는 정보는 아래와 같습니다.

• $B$ 는 9개의 unknown으로 구성되어 있음
• $h$ 는 알고 있음
• 2개의 equation은 $B$ 와 $h$ 로 구성되어 있음

B 구하기

먼저 vector $b$ 를 다음과 같이 정의합니다. B가 symmetric이기 때문에 upper만 구해도 충분하기 때문에 아래와 같이 정의합니다.

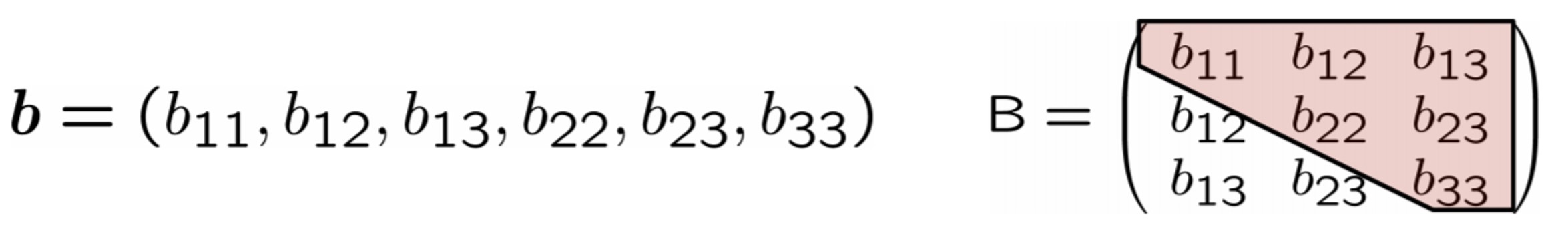
이전의 제약 조건을 적용하여 linear equation system $Vb$ = 0 을 구성합니다.

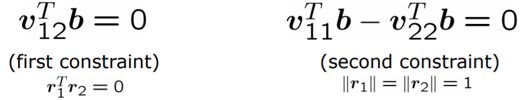
그렇다면 한 개의 이미지에서 우리가 얻은 식은 아래와 같습니다.

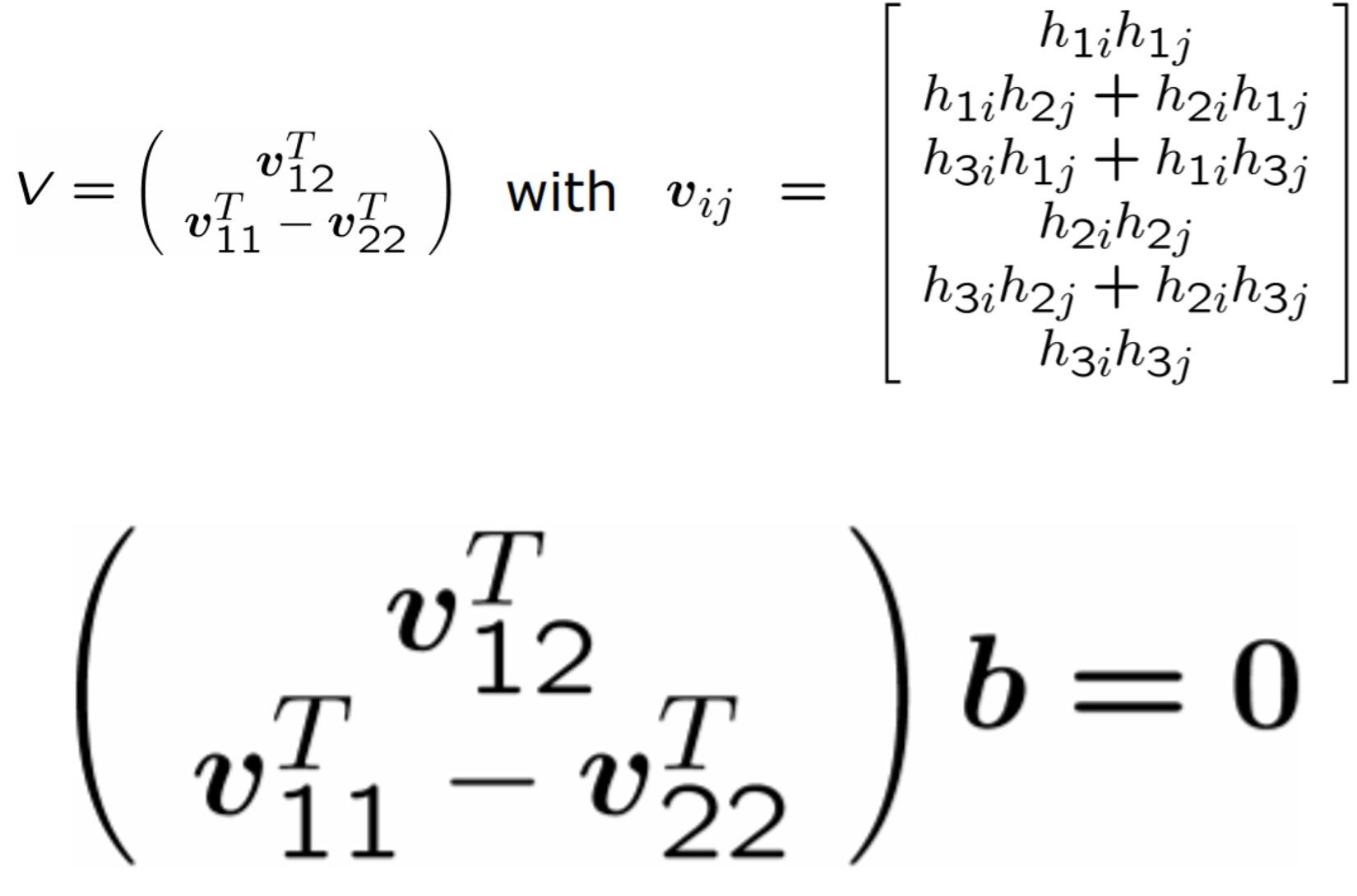
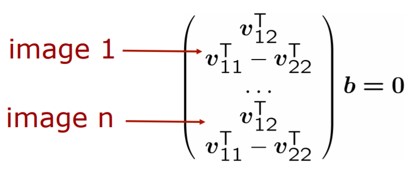
이제 $Vb$ = 0 을 구하기 위해 여러 개의 이미지가 필요하게 됩니다. 여러 개의 이미지를 통해 linear system을 구성한 후 $Vb$ = 0 을 풀어 $B$ 를 얻고 $K$ 를 얻으면 끝나게 됩니다.

제약 조건 및 현실에서의 noise 고려하기

$Vb$ = 0 에서 Trivial solution을 가질 수 있으므로 $\left ||b \right ||$ = 1 제약 조건을 추가하게 되고, 현실에서의 Real measurement는 noisy하므로 square error를 최소화하는 solution을 찾아야 합니다. 아래와 같습니다.

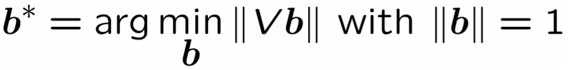
DLT 계산처럼 solve (SVD를 구해서 가장 작은 singular value의 singular vector를 선택)

필요한 것을 다시 요약해봅시다!

• 행렬 H를 구하기 위해 plane 당 최소 4개의 point가 필요하다!
• 각 plane 당 2개의 방정식이 나오게 된다!
• B가 5/6 DoF를 가지기 때문에 plane 의 3가지 view가 필요하다!
  • 각 이미지마다 고유한 H 존재
  • B가 대칭 행렬이고 scaling 계수 모름
• $Vb$ = 0을 풀음으로써 K를 구한다!

따라서 내부 파라미터를 구할 수 있게 됩니다. 위와 같은 camera calibration은 카메라가 pinhole camera를 가정하며 lens에 대한 non-linear distortion은 없다고 가정합니다.(실제로는 먼저 non-linear distortion을 잡고 진행하게 됩니다.)